Диагональ равносторонней трапеции равна 60 градусам перпендикулярно боковой стенке. Если большое основание равно 8√3, а трапеция находится под одним острым углом, найдите площадь трапеции. (переводил в переводчике)

Диагональ равносторонней трапеции равна 60 градусам перпендикулярно боковой стенке. Если большое осн

Показать ответ

Ответ:

elyakhina1976

18.03.2020 01:55

68. По данным на рисунке найдите площадь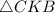 $\triangle CKB$ .

- - -Дано :

ΔСКВ - прямоугольный (∠С = 90°).

СК - высота (СК⊥АВ).

АК = 4, КВ = 16.

Найти : $S_{\triangle CKB} ~=~ ?$ Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.

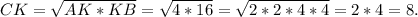
Следовательно, $CK = \sqrt{AK*KB} = \sqrt{4*16} = \sqrt{2*2*4*4} = 2*4 = 8.$

Площадь прямоугольного треугольника равна половине произведения его катетов.

Следовательно,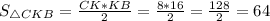 $S_{\triangle CKB}=\frac{CK*KB}{2} =\frac{8*16}{2} =\frac{128}{2} =64$ ед².

ответ :

64 ед².

- - -

70. ABCD - прямоугольник. Найдите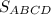 $S_{ABCD}$ .

- - -Дано :

Четырёхугольник ABCD - прямоугольник.

АС - диагональ.

HD⊥АС.

HD = 6, АН = 9.

Найти :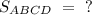

$S_{ABCD}~=~ ?$

Решение :Прямоугольник - это параллелограмм, все углы которого прямые.

Следовательно ∠D = 90°.

Рассмотрим ΔACD - прямоугольный.

В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.

Следовательно,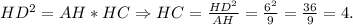 $HD^{2} = AH*HC \Rightarrow HC = \frac{HD^{2} }{AH} = \frac{6^{2} }{9} = \frac{36}{9} =4.$

Площадь треугольника равна половине произведения высоты и стороны, на которую опущена эта высота.

Следовательно,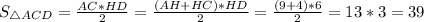 $S_{\triangle ACD}=\frac{AC*HD}{2} =\frac{(AH+HC)*HD}{2} =\frac{(9+4)*6}{2} = 13*3=39$ ед².

Диагональ параллелограмма делит параллелограмм на два равновеликих (равных по площади) треугольника.

Тогда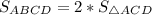 $S_{ABCD} = 2*S_{\triangle ACD}$ = 2*39 ед² = 78 ед².

ответ :

78 ед².

0,0(0 оценок)

Ответ:

wwwcom1

19.06.2021 21:27

Периметр равен P=2*(a+b)

12) P1 = 2*(6+4)=20 P2 = 2*(11.5+7)=37

13) Пусть а=12,4, следовательно b1 = 12.4 - 0.8 = 11.6, b2 = 12.4 + 1.6 = 14, b3 = 12.4 / 4 = 3.1. Тогда P1 = 2*(12.4+11.6) = 48? P2 = 2*(12.4 + 14) = 52.8, P3= 2*(12.4+3.1)=31

14) Так как P=2*(a+b), следовательно a+b = P/2. Тогда 3 + b = 9.2 и b = 9.2-3=6.2. 7 + b = 9.2, тогда b = 9.2 - 7 = 2.2

15) P=24 a1=x, b1 = x+4, следовательно 24 = 2*(x+x+4), 12 = 2x +4, 2x=8, x=4. Тогда a = 4, b = 8. P=24 a1=x, b1 = x-6, следовательно 24 = 2*(x+x-6), 12 = 2x -6, 2x=18, x=9. Тогда a = 9, b = 3. P=24 a1=x, b1 = 2x, следовательно 24 = 2*(x+2x), 12 = 3x, x=4. Тогда a = 4, b = 8.

16) a+b = 12 и a:b = 1:2, следовательно a=x b =2x, тогда x+2x=12, x=4 и a=4 b = 8

a+b = 12 и a:b = 3:2, следовательно a=3x b =2x, тогда 3x+2x=12, x=2.4 и a=7.2 b = 4.8

17)в параллелограмме противоположные углы равны,а односторонние в сумме дают 180 градусов. Следовательно в параллелограмме два угла по 42 градуса и 2 угла по 180-42 = 138 градусов.

0,0(0 оценок)

Популярные вопросы: Геометрия