Диагонали равнобедренной трапеции точкой пересечения делятся в отношении 2 5 вычеслите пириметр трапеции меньшее основание которой равно высоте и составляет 8 см

ответ:ответ: центральный угол AOB равен 110 градусов.

Объяснение:Центральный угол — угол с вершиной в центре окружности.

1) OB - радиус, проведенный в точку касания: касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

Значит угол OBK равен 90 градусов.

2) Углы KBO, ABO и угол в 55 градусов смежные, равны 180 градусов.

Угол ABO = 180-(55+90) = 35 градусов

3) AO=OB, т. к. это радиусы окружности;

Значит треугольник AOB равнобедренный, т. к. боковые стороны AO и OB равны, кроме того и углы при основании равны.

Значит угол ABO = углу OAB = 35 градусов.

4) Из теоремы о сумме углов в треугольнике центральный угол AOB = 180-(35+35) = 110 градусов.

ответ: центральный угол AOB равен 110 градусов.

<2 в два раза больше <1

Объяснение:

1) Т.к. вершина <1 лежит на окружности, а его стороны пересекают окружность, то <1 - вписанный и равен половине дуги на которую опирается.

<1 опирается на дугу AC (по чертежу), следовательно ∪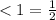

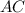
2) Вершина <2 лежит в центре окружности, а стороны угла - радиусы окружности, следовательно <2 - центральный. Известно, что центральный угол равен величине дуги на которую опирается. По чертежу видно, что <2 опирается на дугу AC, т.е ∪ .

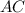3) <1 равен половине дуги AC, а <2 равен целой дуге AC, следовательно  <2 в 2 раза больше <1