Диагонали равнобедренной трапеции взаимно перпендикулярны. Дока- жите, что расстояние между прямыми, содержащими основания, равно
длине средней линии трапеции.

12см расстояние от точки до плоскости треугольника.

Объяснение:

а=8см основание треугольника

h=8см высота треугольника

с=13см расстояние от точки до вершин треугольника

b=? боковая сторона треугольника

S∆=? площадь треугольника

R=? радиус описанной окружности вокруг треугольника

Н=? расстояние от точки к плоскости треугольника

S∆=1/2*a*h=1/2*8*8=32см площадь треугольника.

Высота равнобедренного треугольника является медианой.

По теореме Пифагора найдем боковую сторону треугольника.

b=√((a/2)²+h²)=√((8/2)²+8²)=√(16+64)=√80=

=4√5см боковая сторона треугольника

R=(a*b*b)/4S∆=(8*4√5*4√5)/(4*32)=

=640/128=5см радиус описанной окружности

Теорема Пифагора

с=13см ребро пирамиды

Н=√(с²-R²)=√(13²-5²)=√(169-25)=12см высота пирамиды

1. Правильный четырехугольник - квадрат. 

Диаметр вписанной в квадрат окружности равен стороне квадрата. ⇒ r=d:2=4:2=2 см. 

Для описанного вокруг данной окружности треугольника АВС она - вписанная. 

Радиус вписанной в правильный треугольник окружности равен 1/3 его высоты. Следовательно, высота  ∆ АВС =2•3=6 см. 

Тогда АВ=ВН:sin60°=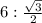=4√3 см. 

              * * *

2. Для нахождения площади сектора существует формула. 

S=Lr:2, где L – длина дуги сектора. ⇒

S=6•4:2=12 см²

Если формула забыта, решить задачу можно без нее. 

 Длина окружности C=2πr

C=2•p•4=8π см

Площадь окружности S=πr²=16 π см²

Вычислим площадь, которая приходится на  сектор с дугой в 1 см.

S:C=16π:8π=2 

Тогда площадь сектора

S=2•6=12 см²