Формула вычисления суммы углов многоугольника такова:
Как мы видим — число не целое, что и означает, что правильный многоугольник, чъя сумма углов равна 1360° — не сущестувет.
б)
Фромула вычисления внуреннего угла в правильном многоуольнике такова:
Количество углов — 18, сумма углов: (18-2)180 = 2880°, каждый внутренний угол равен: 160°.
Да, такой многоугольник может существовать.
в)
Нет, наоборот: радиус описанной окружности больше радиуса вписанной окружности.
Например есть теорема, что радиус описанной окружности около правильного треугольника — в 2 раза больше радиуса вписанной окружности в этот же треугольник.
Один из концов радиуса описанной окружности — не лежит на нём, и не находится в мноугольнике, в то время как радиус вписанной окружности — можно провести через вершины многоугольника до центра окружности.
1. Верно ли утверждение: "Четырехугольник является правильным, если все его углы равны между собой"?
б) нет, так как должны быть равны и стороны, иначе это может быть прямоугольник.
2. Все стороны многоугольника являются хордами окружности. Можно ли утверждать, что многоугольник описан около окружности?
б) нет, этот многоугольник вписан в окружность.
3. Чему равна дуга окружности (в градусах), стягиваемая стороной правильного треугольника?
б) 120° (360° : 3) .
4. Сколько сторон имеет правильный многоугольник, у которого сумма всех его углов равна 540°?
Сумма углов многоугольника равна 180°(n - 2), где n - количество сторон.
180°(n - 2) = 540°
n - 2 = 3
n = 5
а) 5.
5. Чему равна длина окружности, если ее диаметр равен 50 см?
С = πd = 50π см
а) 50π см.
6. Из круга, радиус которого равен 20 см, вырезан сектор. Дуга сектора равна 90°. Чему равна площадь оставшейся части круга?
Дуга оставшейся части круга:
α = 360° - 90° = 270°
Sсект = πR² · α / 360°
Sсект = π · 400 · 270° / 360° = 300π см²
а) 300π см²
а)
Сейчас поэкспериментируем!
Формула вычисления суммы углов многоугольника такова: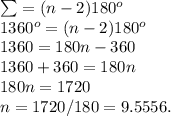
Как мы видим — число не целое, что и означает, что правильный многоугольник, чъя сумма углов равна 1360° — не сущестувет.
б)
Фромула вычисления внуреннего угла в правильном многоуольнике такова:
Количество углов — 18, сумма углов: (18-2)180 = 2880°, каждый внутренний угол равен: 160°.
Да, такой многоугольник может существовать.
в)
Нет, наоборот: радиус описанной окружности больше радиуса вписанной окружности.
Например есть теорема, что радиус описанной окружности около правильного треугольника — в 2 раза больше радиуса вписанной окружности в этот же треугольник.
Один из концов радиуса описанной окружности — не лежит на нём, и не находится в мноугольнике, в то время как радиус вписанной окружности — можно провести через вершины многоугольника до центра окружности.