Сторона меньшего основания правильной треугольной усечённой пирамиды равна 2 см, а боковое ребро пирамиды, равное √2 см , образует со стороной большего основания угол 45° . Найдите полную поверхность пирамиды.
Объяснение:
S( полное)=S(в.осн.)+S(н.основ)+S(бок) ,
1) S(прав.треуг.)= , S(в.осн.)= =√3 (см²).
2)Боковые грани - равнобедренные трапеции . Пусть в трапеции
ВСС₁В₁ отрезки В₁Н, С₁К- высоты. Тогда ΔВВ₁Н-прямоугольный ,равнобедренный (∠ВВ₁Н=90°-45°=45°)⇒ВН=В₁Н=х. По т. Пифагора х²+х²=(√2)² ,х=1. Значит В₁Н=1 , ВС=ВН+НК+КС=1+2+1=4 (см).
1) а=8, b=10, с=12. d=? Sполн=? V=?
V=abc=8*10*12=960
S=2(ab+bc+ac)=2(80 + 120 + 96) = 592
d^2 = a^2+b^2+c^2
d^2= 64 + 100 + 144=308
d=2sqrt{77}
2) a= 18,l= 40. L=?, Sполн=?, V=?
L^2 = 40^2 + 9^2 = 1681
L=41
Sполн= 18^2 + 4 * 1/2 * 40 * 9 = 1044
V = 1/3 * H * 18^2 = 1/3 * sqrt{1033} * 324 = 108sqrt{1033}
3) R= 7, L=11.Sос сеч=?, Sпов=?, V=?
Soc=1/2 * 14 * 11=77
Sпов=ПR(R+L)=П*7(7+11)=126П
V=1/3 * П * 49 * 6sqrt{2} = 98sqrt{2}П
4) a=12, b=15. Sпов=?
Sпов=2*П*12*(12+15)=648П
5) alpha =30 градусов, h= 15 см. Sпов=?
S=2ПRh=2П*5sqrt{3}*15=150sqrt{3}П
Сторона меньшего основания правильной треугольной усечённой пирамиды равна 2 см, а боковое ребро пирамиды, равное √2 см , образует со стороной большего основания угол 45° . Найдите полную поверхность пирамиды.
Объяснение:
S( полное)=S(в.осн.)+S(н.основ)+S(бок) ,
1) S(прав.треуг.)=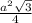
, S(в.осн.)=
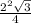=√3 (см²).
2)Боковые грани - равнобедренные трапеции . Пусть в трапеции
ВСС₁В₁ отрезки В₁Н, С₁К- высоты. Тогда ΔВВ₁Н-прямоугольный ,равнобедренный (∠ВВ₁Н=90°-45°=45°)⇒ВН=В₁Н=х. По т. Пифагора х²+х²=(√2)² ,х=1. Значит В₁Н=1 , ВС=ВН+НК+КС=1+2+1=4 (см).
3) S(н.осн.)=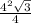
=4√3 (см²).
4)S(бок) =3*S(трапеции ВСС₁В₁) =3* 1/2*В₁Н*(ВС+В₁С₁)=3*1/2*1*6=9(см²).
5)S( полное)=√3 +4√3 +9=9+5√3 ( см²) .