Докажите что AB равен CD если BC параллельно AD и AB параллельно CD на рисунке 1​

1) V =32P см кубических Sбок = 32P см квадратных Sобщ  = 36P см квадратных

2) V = 30P см кубических  Sбок = 98.34 см квадратных   Sобщ = 126.6 см квадратных

3) V =  8P см кубических   S = 16P  см квадратных

Объяснение:

1) Sбок = 2PRh

Sбок = 2*8*4/2*P = 32P см квадратных

Sобщ = Sбок + Sосн

Sосн = PR в квадрате

Sосн = 4P см квадратных

Sобщ = 32P+4P = 36P см квадратных

V = Sосн*h

V = 4P*8 = 32P см кубических

2) Sбок = PRL

L = = =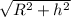

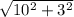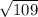
Sбок = 3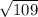P = 98.34 см квадратных

Sосн = PR в квадрате

Sосн = 9P = 28.26 см квадратных

Sобщ = Sбок + Sосн

Sобщ = 98.34 +28.26 =126.6 см квадратных

V = 1/3*P*h*R в квадрате

V = 1/3*P*10*9 = 30P см кубических

3) V = PR в кубе

V = (4/2)в кубе *P = 8P см кубических

S = 4PR в квадрате

S = 16P  см квадратных

1) Обозначим высоту конуса МО, сечение - МАВ.

 МО=АО=R 

Угол АОМ=60°, ⇒∆ АОВ равносторонний. 

АВ=R

MH - высота сечения. 

S(AMB)=AB•MH:2

МН⊥АВ, ⇒ из т. о 3-х перпендикулярах  ОН⊥АВ, ⇒ ОН - высота ∆ АОВ. 

OH=R•sin60°=R√3/2

Из ∆ МOН по т.Пифагора 

МН=√(OM²+OH²)MH=√{R²+3R²/4)=R√(7/4)

————

2) 

AA' -  дуги сектора 120°. Её длина – длина окружности основания конуса. 

Длина AA’  равна 1/3 длины окружности=2πR:3

AA’=24π/3=8π

В конусе

Формула объема конуса  V=S•h/3

S=πr*

r=AA'/2π – r=8π:2π=4

S=π4*=16π

Образующая конуса l=ОА=12

По т.Пифагора 

h=√(AA’*-r*)=√(144-16)=8√2

V=16π•8√2:3=:3=128√2•π/3