Находим координаты точки М: это середина отрезка АС, значит координаты- полусумма соответствующих координат: (2;0;3)
находим координаты вектора ВМ. вычисляя координаты мы вычитаем из координат конца вектора соответствующие координаты точки начала вектора, получаем {-1;0;1}
вычисляем координаты вектора АС по тому же принципу, получаем {-2;4;4}
вычисляем скалярное произведение этих двух векторов по формуле, содержащей сумму произведений соответствующих координат векторов, получаем 6.
вычисляем скалярное произведение по другой формуле, содержащей произведение длин векторов и косинуса угла между ними. Получаем: 6*корень из двух*косинус между векторами АС и ВМ.
Приравниваем два этих ответа и получаем, что косинус равен корень из двух делить на два. это табличное значение косинуса, поэтому угол между вкторами равено 45 градусам
Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти)
уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2
;
R=20 или R=4
значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат
и
вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр
Ищем координаты середины отрезка АВ,
(0;2)
ищем уравнение пряммой АВ в виде y=kx+b
3=-2k+b;
1=2k+b;
2=-4k
1=2k+b;
k=-0.5
b=2;
y=-0.5x+2
перпендикулярные пряммые связаны соотношением угловых коэффициентов
Находим координаты точки М: это середина отрезка АС, значит координаты- полусумма соответствующих координат: (2;0;3)
находим координаты вектора ВМ. вычисляя координаты мы вычитаем из координат конца вектора соответствующие координаты точки начала вектора, получаем {-1;0;1}
вычисляем координаты вектора АС по тому же принципу, получаем {-2;4;4}
вычисляем скалярное произведение этих двух векторов по формуле, содержащей сумму произведений соответствующих координат векторов, получаем 6.
вычисляем скалярное произведение по другой формуле, содержащей произведение длин векторов и косинуса угла между ними. Получаем: 6*корень из двух*косинус между векторами АС и ВМ.
Приравниваем два этих ответа и получаем, что косинус равен корень из двух делить на два. это табличное значение косинуса, поэтому угол между вкторами равено 45 градусам
ответ: 45 градусов
Так как окружность касания осей координат, то для координат ее центра и радиуса окружности справделиво равенство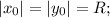 учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти)
учитывая, что окружность проходит через точку (8;-4) опускаем модуль (окружность за исключением точек касания находится в IV четверти) 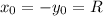
уравнение окружности имеет вид (x-x_0)^2+(y-y_0)^2=R^2
R=20 или R=4
значит существуют две окружности проходящие через точку (8;-4) и касающееся осей координат
и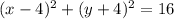
вторая задача, пряммая симетричная относительно точек А и В - середнинный перпендикуляр
Ищем координаты середины отрезка АВ,
(0;2)
ищем уравнение пряммой АВ в виде y=kx+b
3=-2k+b;
1=2k+b;
2=-4k
1=2k+b;
k=-0.5
b=2;
y=-0.5x+2
перпендикулярные пряммые связаны соотношением угловых коэффициентов
k_1k_2=-1
поєтому угловой коєффициент искомой пряммой равен k=-1/(-0.5)=2
учитывая что искомая пряммая проходит через точку С ищем ее уравнение в виде
y=kx+b (k=2)
2=2*0+b;
b=2
y=2x+2 или y-2x-2=0
в чем ошибка у вас - неведомо, ибо вы своего решения не предоставили