Докажите методом от противного, что не существует - вопрос №312958 от daniilgurnyy 31.01.2021 11:14

Question

Геометрия: Докажите методом от противного, что не существует треугольника, в котором медиана к одной стороне равна полсумме двух других сторон

daniilgurnyy · Answer

Рассмотрим треугольник с основанием c, боковыми сторонами a и b, и медианой к основанию m. Обозначим угол наклона медианы к основанию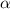 $\alpha$ со стороны a, и 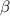$\beta$ со стороны b.

По теореме косинусов:

$a^2=m^2+\frac{c^2}{4}-mc \cdot \cos \alpha\\ b^2=m^2+\frac{c^2}{4}-mc \cdot \cos \beta=m^2+\frac{c^2}{4}+mc \cdot \cos \alpha$

То есть

$a^2+b^2=2m^2+\frac{c^2}{2}\\ 2a^2+2b^2=4m^2+c^2$

Предположим от противного, что медиана к основанию равна полусумме боковых сторон:

$2m=a+b\\ 4m^2=a^2+2ab+b^2$

Подставив выражение для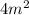 4m^2 в предыдущее равенство, получим:

$2a^2+2b^2=a^2+2ab+b^2+c^2\\ a^2-2ab+b^2=c^2\\ (a-b)^2=c^2\\ a-b=c\\ a=b+c$

То есть сумма двух сторон треугольника равна его третьей стороне.

Поскольку такого треугольника не существует, следовательно исходное предположение неверно, и медиана к одной стороне треугольника не может равняться полусумме двух других его сторон.