Воспользуемся таблицами Брадиса В.М. для синусов и косинусов углов.
Для нахождения косинусов углов таблицу используем снизу вверх, значения углов берем из правой колонки, значения минут из нижней строки.
Находим значение cos 71° 0' (см. приложение 1).
cos 71° = 0,3256.
2) Найти cos 18° 25'.
Находим по таблице косинусов в правой колонке угол 18°.
В нижней строке нет значения 25', поэтому берем ближайшее значение минут: 24', и сделаем поправку на 1 минуту. Поправка равна 1 (см. приложение 2).
cos 18° 24' = 0,9489.
Так как с увеличением острого угла значение косинуса уменьшается, то поправку нужно отнять.
9489 - 1 = 9488.
Тогда cos 18° 25' = 0,9488.
3) Найти радиус описанной около треугольника окружности, если известен угол треугольника ∠A = 60° и длина противолежащей стороны BC = 14 см. Рисунок прилагается (приложение 3).
Радиус описанной окружности найдем по формуле:
где R - радиус описанной окружности, a - сторона треугольника, α - противолежащий этой стороне угол.
Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.
а) По теореме Пифагора:
AC = √(AB² - BC²) = √(17² - 8²) = √(289 - 64) = √225 = 15
sin∠A = BC / AB = 8/17 sin∠B = AC / AB = 15/17
cos∠A = AC / AB = 15/17 cos∠B = BC / AB = 8/17
tg∠A = BC / AC = 8/15 tg∠B = AC / BC = 15/8
б) По теореме Пифагора:
АВ = √(BC² + AC²) = √(21² + 20²) = √(441 + 400) = √841 = 29
sin∠A = BC / AB = 21/29 sin∠B = AC / AB = 20/29
cos∠A = AC / AB = 20/29 cos∠B = BC / AB = 21/29
tg∠A = BC / AC = 21/20 tg∠B = AC / BC = 20/21
в) По теореме Пифагора:
АВ = √(BC² + AC²) = √(1² + 2²) = √(1 + 4) = √5
sin∠A = BC / AB = 1/√5 sin∠B = AC / AB = 2/√5
cos∠A = AC / AB = 2/√5 cos∠B = BC / AB = 1/√5
tg∠A = BC / AC = 1/2 tg∠B = AC / BC = 2
г) По теореме Пифагора:
ВС = √(АВ² - AC²) = √(25² - 24²) = √(625 - 576) = √49 = 7
sin∠A = BC / AB = 7/25 sin∠B = AC / AB = 24/25
cos∠A = AC / AB = 24/25 cos∠B = BC / AB = 7/25
tg∠A = BC / AC = 7/24 tg∠B = AC / BC = 24/7
1) cos 71° = 0,3256.
2) cos 18° 25' = 0,9488.
3) Радиус описанной окружности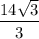 см.
см.
Объяснение:
1) Найти cos 71°.
Воспользуемся таблицами Брадиса В.М. для синусов и косинусов углов.
Для нахождения косинусов углов таблицу используем снизу вверх, значения углов берем из правой колонки, значения минут из нижней строки.
Находим значение cos 71° 0' (см. приложение 1).
cos 71° = 0,3256.
2) Найти cos 18° 25'.
Находим по таблице косинусов в правой колонке угол 18°.
В нижней строке нет значения 25', поэтому берем ближайшее значение минут: 24', и сделаем поправку на 1 минуту. Поправка равна 1 (см. приложение 2).
cos 18° 24' = 0,9489.
Так как с увеличением острого угла значение косинуса уменьшается, то поправку нужно отнять.
9489 - 1 = 9488.
Тогда cos 18° 25' = 0,9488.
3) Найти радиус описанной около треугольника окружности, если известен угол треугольника ∠A = 60° и длина противолежащей стороны BC = 14 см.
Рисунок прилагается (приложение 3).
Радиус описанной окружности найдем по формуле:
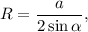
где R - радиус описанной окружности, a - сторона треугольника, α - противолежащий этой стороне угол.
По таблице:
Подставим данные задачи:
Радиус описанной окружности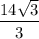 см.
см.