2. Высота поделила основу пополам,тем самым поделив треугольник на 2 маленьких.По теореме Пифагора квадрат гипотенузы = сумме квадратов катетов. Найдём катет( половину основы треугольника).
225 = 81 +
= 225 - 81 = 144
х = = 12 см
Теперь узнаем длинну основы: 12 +12 = 24 см
3.Площадь ромба через его сторону и угол
S = a²·sin(β) = (7√2)²·sin(135°) = 49*2 * 1/√2 = 49√2 см
4. Не знаю, прости((((
5.Дано: трапеція КМРТ, МР=7 см, КТ=9 см, ∠Т=45°.
Проведемо висоту РН. Розглянемо ΔРТН - прямокутний.
∠Т=45°, тоді ∠ТРН=90-45=45°, тобто ΔРТН - рівнобедрений.
Точка M равноудалена от сторон ромба и находится на расстоянии 2 см от плоскости ромба. Найдите расстояние от точки M до стороны ромба, если его диагонали равны 16 см и 12 см.
-------
Обозначим ромб АВСД,
Расстояние от точки до прямой равно длине отрезка, проведённого перпендикулярно от точки к данной прямой. =>
отрезок МН перпендикулярен сторонам ромба. МН⊥АВ.
Расстояние от точки до плоскости - длина перпендикуляра между точкой и плоскостью. ⇒ МО перпендикулярен каждой прямой, проходящей через О в плоскости ромба.
т.М равноудалена от сторон ромба, =>
длина проекции ОН отрезка МН равна радиусу вписанной в этот ромб окружности, т.е. ОН равен половине высоты ромба.
а) Диагонали ромба пересекаются под прямы углом и делят его на равные прямоугольные треугольники с катетами, равными их половине.
1. 12 * 7 = 84 см"
2. 24 см
3.49√2 см
4. -----------
5.24√2 см²
Объяснение:
1. Тут и так понятно)
2. Высота поделила основу пополам,тем самым поделив треугольник на 2 маленьких.По теореме Пифагора квадрат гипотенузы = сумме квадратов катетов. Найдём катет( половину основы треугольника).
225 = 81 +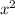
х =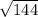
= 12 см
Теперь узнаем длинну основы: 12 +12 = 24 см
3.Площадь ромба через его сторону и угол
S = a²·sin(β) = (7√2)²·sin(135°) = 49*2 * 1/√2 = 49√2 см
4. Не знаю, прости((((
5.Дано: трапеція КМРТ, МР=7 см, КТ=9 см, ∠Т=45°.
Проведемо висоту РН. Розглянемо ΔРТН - прямокутний.
∠Т=45°, тоді ∠ТРН=90-45=45°, тобто ΔРТН - рівнобедрений.
Нехай РН=ТН=х см, тоді за теоремою Піфагора
х²+х²=6²; 2х²=36; х²=18; х=√18=3√2; РН=3√2 см.
S=(МР+КТ):2*3√2=(7+9)/2*3√2=24√2 см²
Точка M равноудалена от сторон ромба и находится на расстоянии 2 см от плоскости ромба. Найдите расстояние от точки M до стороны ромба, если его диагонали равны 16 см и 12 см.
-------
Обозначим ромб АВСД,
Расстояние от точки до прямой равно длине отрезка, проведённого перпендикулярно от точки к данной прямой. =>
отрезок МН перпендикулярен сторонам ромба. МН⊥АВ.
Расстояние от точки до плоскости - длина перпендикуляра между точкой и плоскостью. ⇒ МО перпендикулярен каждой прямой, проходящей через О в плоскости ромба.
т.М равноудалена от сторон ромба, =>
длина проекции ОН отрезка МН равна радиусу вписанной в этот ромб окружности, т.е. ОН равен половине высоты ромба.
а) Диагонали ромба пересекаются под прямы углом и делят его на равные прямоугольные треугольники с катетами, равными их половине.
По т.Пифагора АВ=√(ОН²+ОВ²)=√(36+64)=10 см
б) По ТТП МН⊥АВ => ОН⊥АВ.
ОН можно найти из площади ∆ АОВ
Ѕ(АОВ)=ОА•ОВ:2=24
ОН=24•2:2=4,8
По т.Пифагора МН=√(MO²+OH²)=√(4+23,04)=5,2 см