Дві сторони трикутника 25 см і 30 см. Знайдіть висоту трикутника, проведено на третю його сторону, яка дорівнює 11 см

Ч.т.д.

Объяснение:

Расстояние от точки до прямой - это длина перпендикуляра, проведённого из данной точки к этой прямой.

Так как пирамида правильная, значит её боковые грани представляют собой равнобедренные треугольники.

А это значит, что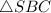 - равнобедренный.

И по свойству равнобедренного треугольника,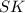 - медиана, биссектриса, высота .

, то есть - расстояние от точки S до BC.

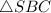По условию,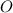 - середина .

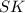Значит .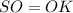

Также по условию,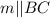 и m ∈ (SBC) .

- расстояние от S до m, а - расстояние от m до BC.

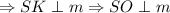Значит, расстояние от точки S до прямой m равно расстоянию между прямыми m и BC.

AC лежит в плоскости основания, ребро СС1 прямоугольного параллелепипеда перпендикулярно плоскости основания. Треугольник ACC1 - прямоугольный с углом 30°.
AC=AC1/2 =√3 (катет против угла 30° равен половине гипотенузы)
CC1=AC√3 =3 (катет против угла 60° равен другому катету, умноженному на √3)

Грани прямоугольного параллелепипеда - прямоугольники.
P(ABCD) =2(AB+BC) =2√5 <=> AB+BC=√5

AB^2 +BC^2 =AC^2 <=>
(AB+BC)^2 =AC^2 +2AB*BC <=>
AB*BC =(5-3)/2 =1

Объем прямоугольного параллелепипеда равен призведению трех его измерений:
V=AB*BC*CC1 =3