Высота в равнобедренном треугольнике является одновременно и медианой, и биссектрисой. Медиана, проведённая из вершины угла в противоположную сторону, делит её на две равные части. Соответственно, проведённая из противоположного основанию угла высота делит его пополам. Перпендикуляр образует два прямоугольных треугольника. Боковая сторона равнобедренного треугольника представляет из себя гипотенузу. За катет берём получившуюся в результате раздела основания на две равные части сторону. По теореме Пифагора находим оставшийся катет, что и будет выступать в роли высоты.
Находим площадь, умножив основание на высоту и поделив на 2. △ (см²)
Острые углы трапеции равны 20° и 70° .Ее боковые стороны равны 10 и 24 найти длину отрезка, который соединяет середины оснований трапеции.
Объяснение:
Пусть AB=10 ,CD=24 ,∠A=70°,∠D=20° ,К-середина ВС, Н-середина АD .
1) Проведем через точку К прямую КО||AB и КЕ||CD. Тогда
-КО=АВ=10 как противоположные стороны параллелограмма АВКО и ВК=АО;
- КЕ=CD=24 как противоположные стороны параллелограмма DCKH и КС=DE.
Поэтому ОН=НЕ как разность равных отрезков.
2) Т.к.КО||AB , то ∠ВАD=∠KOH=70° как соответственные при секущей АD. Тк. КЕ||CD , то ∠СDА=∠KЕH=20° как соответственные при секущей АD.
В ΔОКЕ ∠OKE=180°-70°-20°=90°⇒ΔОКЕ прямоугольный . Отрезок КН- медиана , а значит радиус описанной окружности .
R=0,5OE =0,5√(ОК²+КЕ²)=0,5√(576+100)=0,5*26=13 (ед).
Пошаговое решение:
Дано: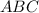 ;
;
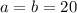 см;
см;
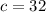 см;
см;
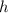 - высота;
- высота;
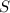 △
△ ;
;
 равнобедренного треугольника представляет из себя гипотенузу. За катет берём получившуюся в результате раздела основания на две равные части сторону. По теореме Пифагора находим оставшийся катет, что и будет выступать в роли высоты.
равнобедренного треугольника представляет из себя гипотенузу. За катет берём получившуюся в результате раздела основания на две равные части сторону. По теореме Пифагора находим оставшийся катет, что и будет выступать в роли высоты.
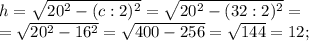
 △
△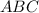
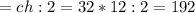 (см²)
(см²)
△
Найти:
Решение:
Высота в равнобедренном треугольнике является одновременно и медианой, и биссектрисой. Медиана, проведённая из вершины угла в противоположную сторону, делит её на две равные части. Соответственно, проведённая из противоположного основанию угла высота делит его пополам. Перпендикуляр образует два прямоугольных треугольника. Боковая сторона
Находим площадь, умножив основание на высоту и поделив на 2.