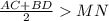Находим координаты направляющего вектора прямой NM:
NM: (1; 1; 1).
Принимаем координаты направляющего вектора прямой NM как соответствующие координаты нормального вектора n плоскости α :
n = (A; B; C). То есть, A = 1, B = 1, C = 1.
Записываем уравнение плоскости, проходящей через точку А(2; 1; 0) и имеющей нормальный вектор n(A; B; C), в виде:
A(x -x1) + B(y - y1) + C(z - x1) - это и есть искомое уравнение плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой.
Рассмотрим четырехугольник ABCD; Пусть в нем диагональ AC зафиксирована, то есть имеет постоянную длину. Минимальная полусумма диагоналей получается тогда, когда вторая диагональ имеет нулевую длину. В таком случае точка B переходит в точку D. Рассмотрим отрезок MN - тот, что соединяет середины сторон BC и AD. Он сместился в точку M', причем MN ║ BD, поскольку B сместилась в D. Точка N осталась на прежнем месте. Получили треугольник ACD в котором M'N - средняя линия. Поэтому , но мы рассматриваем четырехугольник, никакие две вершины которого не лежат друг на друге. Значит, в остальных случаях
Даны : А(2,1,0), М(3,-2,1), N(2,-3,0).
Находим координаты направляющего вектора прямой NM:
NM: (1; 1; 1).
Принимаем координаты направляющего вектора прямой NM как соответствующие координаты нормального вектора n плоскости α :
n = (A; B; C). То есть, A = 1, B = 1, C = 1.
Записываем уравнение плоскости, проходящей через точку А(2; 1; 0) и имеющей нормальный вектор n(A; B; C), в виде:
A(x -x1) + B(y - y1) + C(z - x1) - это и есть искомое уравнение плоскости, проходящей через заданную точку пространства перпендикулярно к заданной прямой.
Подставляем данные -
α: 1(x -2) + 1(y - 1) + 1z = x + y + z - 3 = 0.
ответ: уравнение плоскости α: x + y + z - 3 = 0.
Рассмотрим четырехугольник ABCD; Пусть в нем диагональ AC зафиксирована, то есть имеет постоянную длину. Минимальная полусумма диагоналей получается тогда, когда вторая диагональ имеет нулевую длину. В таком случае точка B переходит в точку D. Рассмотрим отрезок MN - тот, что соединяет середины сторон BC и AD. Он сместился в точку M', причем MN ║ BD, поскольку B сместилась в D. Точка N осталась на прежнем месте. Получили треугольник ACD в котором M'N - средняя линия. Поэтому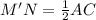
, но мы рассматриваем четырехугольник, никакие две вершины которого не лежат друг на друге. Значит, в остальных случаях 