Две окружности лежат одна вне другой. проведены четыре общие касательные( две внутренние и две внешние). возьмём внешнюю касательную и отрезок на ней между точками касания. этот отрезок делит внутреннюю касательную на три части. длкажите, что две крайние части равны.
Поскольку четырехугольная пирамида ПРАВИЛЬНАЯ, то в основании лежит квадрат. Диагональ квадрата ABCD равен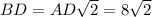
см. Диагонали квадрата пересекаются в точке О и точка О делит диагонали пополам, то есть 
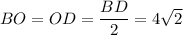см.
Из прямоугольного треугольника SOD: из определения косинуса найдем боковое ребро пирамиды:
Высота SK равнобедренного треугольника SCD делит основание CD пополам, то есть: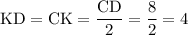
см
Тогда из прямоугольного треугольника SKC:
Площадь боковой поверхности - это сумма всех площади граней. То есть, зная что у правильной пирамиды все грани равны, то площадь бок. пов.
ответ: 64√3 см².
1. 13 см и 13 см
2. AM:AB=1:3 и MB:AB=2:3
Объяснение:
1. Диагонали прямоугольника равны и поэтому достаточно определить длину одной из них, например BD (см. рисунок).
Так как диагональ прямоугольника делит прямоугольник на два прямоугольных треугольника, то для прямоугольного треугольника применим теорему Пифагора:
BD²=AB²+AD² = (5 см)²+(12 см)² = 25 см² + 144 см² = 169 см²=(13 см)²
Отсюда
BD=13 см.
2. Так как отношение AM:MB=1:2, то MB=2·AM. Тогда
AB=AM+MB=AM+2·AM=3·AM.
Поэтому
AM:AB=AM:(3·AM)= 1:3
MB:AB=(2·AM):(3·AM)= 2:3