Две взаимно перпендикулярные прямые проходят через центр квадрата. Докажите, что отрезки этих прямых, ограниченные сторонами квадрата, равны между собой.
Две прямые, перпендикулярные одной и той же плоскости, параллельны.
PP1 ⊥ ,
QQ1 ⊥ => PP1 II QQ1
Через 2 параллельные прямые можно провести плоскость и притом только одну .
PP1 и QQ1 принадлежат одной плоскости B.
Пусть P1Q1 - линия пересечения плоскостей Альфа и Бета.
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Длина окр: 2пr = 8п 2r=8п:п 2r =8 r=4-рдиус вписан. окр. S впис. окр = пr2 S=3,14*4*4= 50,24 - плозадь впис окр. Плозадь окр, опис. вокруг правильного треуг. в 4 раза больше S опис. окр. =50,24*4=200,96 S кольца = S опис. окр.- S впис. окр. S кольца= 200,96- 50,24= 150,72 В треуг ABCD проведем медеаны,AD,BK,CM. S треуг. ABCD 1/2 AC*BK, 1/2 AC=KC Медиана треуг. впис окр. делится в отношении 2:1 Поэтому высота BK=R+r=8+4=12 S=12*KC Найдем KC - сторону треуг. KOC, KC-касат.,OC=R=8-гипотинуза, другой катет ОK=r=4 KC2=OC2+OK2 KC-корень из 8*8-4*4= корень из 48= 6,92 Sтреуг. ABC=12*6,92=83,04 Прости,но без рисунка.
PP1Q1Q-квадрат
Периметр равен 41,2 см
Объяснение:
Две прямые, перпендикулярные одной и той же плоскости, параллельны.PP1 ⊥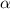 ,
,
QQ1 ⊥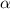 => PP1 II QQ1
=> PP1 II QQ1
Через 2 параллельные прямые можно провести плоскость и притом только одну .PP1 и QQ1 принадлежат одной плоскости B.
Пусть P1Q1 - линия пересечения плоскостей Альфа и Бета.
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.=>PQ II P1Q1
PQQ1P1 - параллелограмм.
Так как < PP1Q1, <QQ1P1 равны 90°, то
PQQ1P1 - прямоугольник.
PP1=PQ => PQQ1P1 - квадрат.
Периметр квадрата находится по формуле:
Р=4а=4×10,3= 41,2 см
2пr = 8п
2r=8п:п
2r =8
r=4-рдиус вписан. окр.
S впис. окр = пr2
S=3,14*4*4= 50,24 - плозадь впис окр.
Плозадь окр, опис. вокруг правильного треуг. в 4 раза больше
S опис. окр. =50,24*4=200,96
S кольца = S опис. окр.- S впис. окр.
S кольца= 200,96- 50,24= 150,72
В треуг ABCD проведем медеаны,AD,BK,CM.
S треуг. ABCD 1/2 AC*BK, 1/2 AC=KC
Медиана треуг. впис окр. делится в отношении 2:1
Поэтому высота BK=R+r=8+4=12
S=12*KC
Найдем KC - сторону треуг. KOC, KC-касат.,OC=R=8-гипотинуза, другой катет ОK=r=4
KC2=OC2+OK2
KC-корень из 8*8-4*4= корень из 48= 6,92
Sтреуг. ABC=12*6,92=83,04
Прости,но без рисунка.