Если гипотенуза и прилежащий острый угол одного треугольника соответственно равны гипотенузе и прилежащему острому углу другого, то такие прямоугольные треугольники равны. Какой это признак?
Второй признак
Четвертый признак
Третий признак
Первый признак
ответ: 25√3 см².
Объяснение:
∠CAD = 30° - по условию; AC = 10 см.
∠BCA = ∠CAD = 30° как накрест лежащие при AD║BC и секущей АС.
Из вершины А проведем перпендикуляр до пересечения с продолжением стороны ВС, см. рисунок.
Из прямоугольного треугольника AHC: против угла 30° катет в два раза меньше гипотенузы, т.е. AH = AC/2 = 10/2 = 5 см
по т. Пифагора: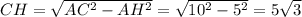 см
см
AD = AE + EF + FD ⇔ AD + BC = AE + EF + BC + FD
AD + BC = AE + EF + EF + FD
Поскольку AE = FD, то AD + BC = 2EF + 2AE = 2(EF+AE)=2CH
AD + BC = 2 * 5√3 = 10√3 см.
Следовательно, высота трапеции будет лежать против угла в 30°, и равна половине диагонали, которая является гипотенузой в треугольнике, отсекаемом высотой, т.е. равна 10/2=5/см/
Второй же катет этого треугольника состоит из верхнего основания и кусочка нижнего, который отсекается высотой от нижнего основания. Но это и будет полусумма верхнего и нижнего оснований, т.к. трапеция равнобедренная. И полусумма эта равна произведению гипотенузы на косинус угла в 30°, т.е. 10*√3/2=5√3/см/
Значит, площадь трапеции равна 5*5√3=25√3/см²/