1. Треугольники DOC и АОВ подобны по первому признаку подобия треугольников: два угла одного треугольника соответственно равны двум углам другого. В нашем случае углы DOC и АОВ равны как вертикальные углы, а углы DCA и САВ равны как накрест лежащие углы при пересечении параллельных прямых DC и АВ секущей АС. 2. Выразим ОС как 15-АО 3. Поскольку треугольники подобны, можно записать: АО / ОС = АВ / DC, АО = ОС*АВ / DC AO = (15-AO)*AB / DC AO = (15-AO)*96 / 24 24AO = (15-AO)*96 24AO = 1440 - 96AO 120AO = 1440 AO = 12 см
Продолжим касательные до их пересечения в т.Р.
ОА⊥АС и О1С⊥АС ( радиусы, проведенные в точку касания.
Из т.О проведем параллельно АС прямую до пересечения с СО1 в т.Н.
Четырехугольник АОНС - прямоугольник. СН=АО=r=12 ⇒
О1Н=20-12=8
⊿ ОНО1 - прямоугольный. ОО1=12+20=32.
По т.Пифагора
ОН=√(OO1²-O1H²)=√(32²-8²)=√960=8√15
cos∠HOO1=OH:OO1=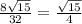
Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.⇒
РС=РD, PA=PB ⇒ BD=AC=8√15
∆ СРD равнобедренный, ∆ РАВ равнобедренный ⇒
биссектриса АО1 перпендикулярна АВ и СD
∠СРО1=∠DPO1
Расстояние между АВ и СD - длина общего между ними перпендикуляра.
Проведем ВМ || РО1
ВМ⊥АВ и ВМ⊥СD.
∆ ВМD прямоугольный. ∠МВD=∠O1PD
ВМ=BD•cosO1PD=8√15•√15:4=30
2. Выразим ОС как 15-АО
3. Поскольку треугольники подобны, можно записать:
АО / ОС = АВ / DC,
АО = ОС*АВ / DC
AO = (15-AO)*AB / DC
AO = (15-AO)*96 / 24
24AO = (15-AO)*96
24AO = 1440 - 96AO
120AO = 1440
AO = 12 см