Если угол колебания маятника настенного часа 38, то какова длина маятника, если длина дуги маятника 24см, то какова длина маятника?

Показать ответ

Ответ:

ALIONA2020

06.09.2021 01:12

а) ∠В = 30°, АВ=4 см, AD=ВD=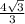 $\frac{4\sqrt{3} }{3}$ см ∠D=120°

б) S = 2√3 cм²

Объяснение:

а) Сумма острых углов прямоугольного треугольника равна 90°

∠В=90°-∠А=90°-60°=30°

Катет прямоугольного треугольника, лежащий напротив угла в 30° равен половине гипотенузы.

⇒ АВ=2*АС=2*2=4см

По теореме Пифагора найдём катет ВС:

$BC=\sqrt{AB^{2}-AC^{2} } =\sqrt{4^{2}-2^{2} } =\sqrt{12} =2\sqrt{3}$

ВС = 2√3 см

Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.

$\dfrac{AB}{BC} =\dfrac{BD}{DC} \\\\\\\dfrac{4}{2} =\dfrac{BD}{2\sqrt{3}-BD } \\\\\\BD=4\sqrt{3} -2BD\\\\3BD=4\sqrt{3} \\\\BD=\dfrac{4\sqrt{3} }{3}$

Рассмотрим ΔABD: ∠ВАD=30° - так как AD – биссектриса, ∠В=30° ⇒ ΔABD- равнобедренный, AD=ВD=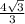 $\frac{4\sqrt{3} }{3}$ см

Так как сумма углов треугольника = 180°, то

∠АDB = 180-∠ВАD-∠В=180-30-30=120°

б) Площадь прямоугольного треугольника равна произведению двух его катетов деленное на 2:

$S = \dfrac{1}{2} *BC*AC=\dfrac{1}{2} *2\sqrt{3} *2=2\sqrt{3}$

S = 2√3 cм²

В треугольнике ABC ∠C = 90°, AD – биссектриса, ∠A = 60°, AC = 2 см. а) Решите треугольник ABD ( ). б

0,0(0 оценок)

Ответ:

макатернар1

10.11.2020 11:23

Сначала делим четырехугольник диагональю на два треугольника.

Находим центр тяжести каждого треугольника как точку пересечения его медиан. Центр тяжести четырехугольника лежит на прямой О1О2, соединяющей центры тяжести этих треугольников.

Затем делим четырёхугольник на 2 треугольника при другой диагонали и находим так же центры тяжести других треугольников. Соединяем их отрезком О3О4.

Искомый центр тяжести четырёхугольника лежит в точке ЦТ пересечения отрезков О1О2 и О3О4.

ABD x y BCD x y

O2 3 2 O3 2 2

ADC x y ABC x y

O1 0,6667 1,3333 O4 3,3333 1,6667

ЦТ = х у

2,533 1,8667