ЭТО СОР НУЖНО СЕГОДНЯ СДАТЬ

а) Изобразите окружность, заданной уравнением: (x −2)^2 + (y −3)^2 =25 .

b) Определите взаимное расположение прямой y = 8 и окружности (x −2)^2 + (y −3)^2 =25
​

Из точки В проведём перпендикуляр ВД к АС . Для этого продолжим АС, поскольку угол ВАС больше 90, это пересечение будет за пределами треугольника. На плоскости L возьмём точку К. Проведём к ней перпендикуляр ВК из В.Это и будет искомое расстояние. ДС ребро двугранного угла образованного плоскостью L и плоскостью АВС.Угол КДВ=30 это линейный угол данного угла. Найдем ВД. Применим теорему Пифагора. ВД это общий катет треугольников ДВА и ДВС. Обозначим ДА=Х. Тогда( АВ квадрат)-(АД квадрат)=(ВС квадрат-ДС квадрат). Или (169-Х квадрат)=((225-(4+Х)квадрат).  169-Хквадрат=225-16 -8Х-Хквадрат. Отсюда Х=АД=5. Тогда ВД =корень из(АВ квадрат-АДквадрат)=корень из(169-25)=12. ВК=ВД*sin30=12*1/2=6.

а) (-2;0) - центр окружности, радиус окружности равен 3.

б) (0; 4) - центр окружности, радиус окружности равен .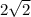

в) (5; -7) - центр окружности, радиус окружности равен 4.

Объяснение:

Уравнение окружности имеет вид: (x-a)²+(y-b)²=R². Здесь центр окружности (a; b) . R - радиус окружности.

а) (-2; 0) -центр окружности, R²=9. R²=3². R=3.

б) (0; 4) - центр окружности, ,  .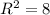

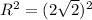
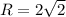в) (5; -7) - центр окружности, R²=16,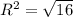 ,  R=4.

Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень