Геометрия 1. Стороны прямоугольника равны 20 и 21. Найти его диагональ.
2. В параллелограмме CDEF сторона CD = 11 см, CF=21см, угол D=150.
Найдите:
1) площадь параллелограмма;
2) высоту, проведённую к большей стороне.
3. Основания в прямоугольной трапеции равны 28 см и 13 см, а большая боковая сторона – 17 см. Найдите площадь трапеции.
4. В треугольнике QRS ∠Q = 45°, RS = 10 см, а высота RH отсекает на стороне QS отрезок HS, равный 8 см. Найдите площадь треугольника QRS.
5. Высота LH параллелограмма KLMN делит его сторону KN на отрезки KH = 7 и HD = 32. Диагональ параллелограмма LN равна 40. Найдите площадь параллелограмма.
6. В равнобедренном прямоугольном треугольнике гипотенуза равна 10 см. Вычислите его площадь.
Дано:
Усеченный конус
Sосн₁ = 9π см²
Sосн₂ = 100π см²
Sсеч = 312π см²
--------------------------------
Найти:
h - ?
1) Сначала мы найдем радиусы окружности верхнего и нижнего усеченного конуса используя площадь круга:
Sосн₁ = πr² ⇒ r = √Sосн₁/π = √9π см²/π = √9 см² = 3 см ⇒ BO₁ = BC = 3 cм
Sосн₂ = πR² ⇒ R = √Sосн₁/π = √100π см²/π = √100 см² = 10 см ⇒ AO = OD = 10 см
2) Равнобедренная трапеция ABCD является осевым сечением данного усеченного конуса: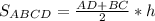
3) В трапеции ABCD:
AD = 2AO = 2R = 2×10 см = 20 см
BC = 2BO₁ = 2r = 2×3 см = 6 см
4) И теперь находим высоту равнобедренной трапеций ABCD:
ответ: h = 24 см
P.S. Рисунок показан внизу↓