Геометрия: геометрия 11 класс с решением

геометрия 11 класс с решением

Показать ответ

Ответ:

basik100grn

18.10.2022 09:09

1)24-6=18 см = а + в, отсюда в=18-а=АВ
медиана в равнобедренном треугольнике является и высотой ,значит треугольник АВД-прямоугольный
следует ,что АВ=в= 18-а является гипотенузой АВД, АД=а -Ккатет АД
исходя из свойств гипотенузы и катета,получаем,что
2 2 2
(18- а) - а = 6
раскроем скобки
2 2
324- 36 а + а - а =36

квадраты а сокращаются
остается 324-36 а=36
отсюда убираем минусы так как с обоих сторон
остается 36 а= 324-36
36а= 288
а=288 : 36
а= 8 см
18- 8 =10 см= АВ=ВС
АС= 8+8=16 так как медиана делит пополам
периметр АВС=10+10+16=36 см

0,0(0 оценок)

Ответ:

Aleksandr31821

16.06.2020 12:28

Проверим, лежит ли точка А(5,-3) на какой-либо заданной высоте. Подставим координаты этой точки в уравнения высот. Если равенство получим верное, то точка лежит на прямой.

$13x+4y-7=13\cdot 5+4\cdot (-3)-7=46\ne 0\\\\2x-y-1=2\cdot 5-(-3)-1=12\ne 0$

Точка А(5,-3) не лежит ни на одной высоте. Для определённости, пусть высота BN имеет уравнение 2х-у-1=0, а высота СМ: 13х+4у-7=0.

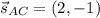BN⊥AC ⇒ направляющий вектор для АС равен нормальному вектору для BN: $\vec{s}_{AC}=(2,-1)$ .

Точка А(5,-3)∈АС и уравнение АС имеет вид:

$\frac{x-5}{2}=\frac{y+3}{-1}\; \; ,\; \; -x+5=2y+6\; \; ,\; \; \underline {x+2y+1=0}$

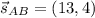CM⊥AB ⇒ направляющий вектор для АВ равен нормальному вектору для CМ: $\vec{s}_{AB}=(13,4)$ .

Точка А(5,-3)∈АВ и уравнение АВ имеет вид:

$\frac{x-5}{13}=\frac{y+3}{4}\; \; ,\; \; 4x-20=13y+39\; \; ,\; \; \underline {4x-13y-59=0}$

Координаты точки В найдём как точку пересечения АВ и BN, а координаты точки С найдём как точку пересечения АС и CM .

$B:\; \left \{ {{4x-13y=59\qquad } \atop {2x-y=1\, |\cdot (-2)}} \right.\oplus \left \{ {{-11y=57} \atop {2x=y+1}} \right. \; \; \left \{ {{y=-\frac{57}{11}} \atop {2x=-\frac{46}{11}}} \right.\; \; \left \{ {{y-\frac{57}{11}} \atop {x=-\frac{23}{11}}} \right. \; \; B(-\frac{23}{11}\, ,\, -\frac{57}{11})\\\\\\C:\; \left \{ {{x+2y=-1\, |\cdot (-2)} \atop {13x+4y=7\qquad }} \right.\oplus \left \{ {{2y=-x-1} \atop {11x=9\quad }} \right. \; \; \left \{ {{2y=-\frac{20}{11}} \atop {x=\frac{9}{11}}} \right.\; \left \{ {{y=-\frac{10}{11}} \atop {x=\frac{9}{11}}} \right.\; \; C(\frac{9}{11}\, ,\, -\frac{10}{11})$