ответ:Номер 1
Треугольник АВD
<ADB=180-(120+40)=20 градусов
<АDB=<CBD=20 градусов,как накрест лежащие при АD || BC и секущей DB
Треугольник АВD равен треугольнику DBC по 1 признаку равенства треугольников-по двум сторонам и углу между ними
АD=BC;<DBC=<ADB;по условию задачи
DB-общая сторона
Равенство доказано,а это значит,что равны и соответствующие стороны и соответствующие углы
<С=<А=120 градусов
<АВD=<BDC=40 градусов ,согласно равенства треугольников,и ещё они являются накрест лежащими углами при АВ || DC и секущей DB
Если при пересечении двух прямых секущей,накрест лежащие углы равны между собой,то прямые параллельны
АВ||DC;AD||BC:
Номер 2
Треугольники АDB и DBC равны между собой по 1 признаку равенства треугольников-по двум сторонам и углу между ними
<DBC=<ADB;AD=BC;DB-общая сторона
Равенство доказано,а значит
АВ=DC;<BDC=<DBA,cогласил равенству треугольников,а также как накрест лежащие при АВ||DC и секущей DB
Если при пересечении двух прямых секущей накрест лежащие углы равны между собой,то прямые параллельны
Объяснение:
ед²
Дано: ABCD - параллелограмм.
AE = ED; DF = FC.
BE ∩ AC = G; BF ∩ AC = H;
S (ABCD) = 12.
Найти: S (GHFE)
1. Рассмотрим ΔABD и ΔDBC.
⇒ S (ΔABD) = S (ΔDBC) = 12:2 = 6
Аналогично:
S (ΔABC) = S (ΔACD) = 12:2 = 6
2. Рассмотрим ΔABD.
AE = ED (условие) ⇒ВЕ - медиана.
⇒ S (ΔABE) = S (ΔEBD) = 6:2 = 3
3. Рассмотрим ΔDBC.
DF = FC ⇒ BF - медиана.
S (ΔDBF) = S(ΔFBC) = 6:2 = 3
4. Рассмотрим ΔACD.
AE = ED; DF = FC (условие)
⇒ EF - средняя линия.
⇒
5. Найдем площадь ΔEBF.
S (ΔEBF) = S (ABCD) - S(ΔABE) - S(ΔFBC) - S(ΔEFD) =
6. Рассмотрим ΔABD.
BF - медиана (п.3)
⇒ BO = OD ⇒ СО - медиана.
⇒ BH : HF = 2:1
или ВН : BF = 2:3
7. Рассмотрим ΔABD.
Аналогично п.6: BE и AO - медианы.
⇒BG : GE = 2 :1
или BG :BE = 2:3
8. Рассмотрим ΔGBH и ΔEBF.
∠B - общий. ВН : BF = 2:3 (п.6); BG :BE = 2:3 (п.7)
⇒ ΔGBH ~ ΔEBF, k =
Найдем площадь GHFE:
ответ:Номер 1
Треугольник АВD
<ADB=180-(120+40)=20 градусов
<АDB=<CBD=20 градусов,как накрест лежащие при АD || BC и секущей DB
Треугольник АВD равен треугольнику DBC по 1 признаку равенства треугольников-по двум сторонам и углу между ними
АD=BC;<DBC=<ADB;по условию задачи
DB-общая сторона
Равенство доказано,а это значит,что равны и соответствующие стороны и соответствующие углы
<С=<А=120 градусов
<АВD=<BDC=40 градусов ,согласно равенства треугольников,и ещё они являются накрест лежащими углами при АВ || DC и секущей DB
Если при пересечении двух прямых секущей,накрест лежащие углы равны между собой,то прямые параллельны
АВ||DC;AD||BC:
Номер 2
Треугольники АDB и DBC равны между собой по 1 признаку равенства треугольников-по двум сторонам и углу между ними
<DBC=<ADB;AD=BC;DB-общая сторона
Равенство доказано,а значит
АВ=DC;<BDC=<DBA,cогласил равенству треугольников,а также как накрест лежащие при АВ||DC и секущей DB
Если при пересечении двух прямых секущей накрест лежащие углы равны между собой,то прямые параллельны
Объяснение:
Объяснение:
Дано: ABCD - параллелограмм.
AE = ED; DF = FC.
BE ∩ AC = G; BF ∩ AC = H;
S (ABCD) = 12.
Найти: S (GHFE)
1. Рассмотрим ΔABD и ΔDBC.
Любая диагональ параллелограмма делит его на два равных треугольника.⇒ S (ΔABD) = S (ΔDBC) = 12:2 = 6
Аналогично:
S (ΔABC) = S (ΔACD) = 12:2 = 6
2. Рассмотрим ΔABD.
AE = ED (условие) ⇒ВЕ - медиана.
Медиана делит треугольник на два равновеликих треугольника.⇒ S (ΔABE) = S (ΔEBD) = 6:2 = 3
3. Рассмотрим ΔDBC.
DF = FC ⇒ BF - медиана.
S (ΔDBF) = S(ΔFBC) = 6:2 = 3
4. Рассмотрим ΔACD.
AE = ED; DF = FC (условие)
⇒ EF - средняя линия.
Средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четвертой площади исходного треугольника.⇒
5. Найдем площадь ΔEBF.
S (ΔEBF) = S (ABCD) - S(ΔABE) - S(ΔFBC) - S(ΔEFD) =
6. Рассмотрим ΔABD.
BF - медиана (п.3)
Диагонали параллелограмма точкой пересечения делятся пополам.⇒ BO = OD ⇒ СО - медиана.
Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2:1, считая от вершины.⇒ BH : HF = 2:1
или ВН : BF = 2:3
7. Рассмотрим ΔABD.
Аналогично п.6: BE и AO - медианы.
⇒BG : GE = 2 :1
или BG :BE = 2:3
8. Рассмотрим ΔGBH и ΔEBF.
∠B - общий. ВН : BF = 2:3 (п.6); BG :BE = 2:3 (п.7)
⇒ ΔGBH ~ ΔEBF, k =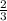
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.Найдем площадь GHFE: