Геометрия: Геометрия, 7 класс решить

Геометрия, 7 класс решить

Показать ответ

Ответ:

egork9957

30.05.2020 19:37

Здание (DF) и башня (CE) находятся на расстоянии 94 м друг от друга. От крыши здания угол возвышения к вершине башни составляет 15°, а угол понижения(склонения) к низу башни - 46°. Вычислите высоту башни ЕС.

ответ:122, 53 м.

Объяснение: очевидно: EC = EB + BC

из ΔDBE: EB = DB*tg(∠EDB) = FCtg15° ;

из ΔDBC: BC =DB*tg(∠CDB) = FCtg46° ;

следовательно: EC = EB + BC = FCtg15°+FCtg46° =FC(tg15°+tg46°) ;

EC =94(tg15°+tg46°)≈94(0,268 +1,0355) =122 , 53 (м) .

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

FC(tg15°+tg46°)≈FC(tg15°+tg45°)=FC((1-cos30°)/sin30°+1 )=FC(3 -√3 ) ;

tg15°=sin15°/cos15=2sin²15°/2sin15°cos15°=(1-cos30°)/sin30° =(1-0,5√3)/0,5 2-√3 ; tg15°+tg45°= 2-√3+1 = 3 -√3 . EC =FC(tg15°+tg45°)=94(3 -√3)

* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

0,0(0 оценок)

Ответ:

Jessabelle

13.09.2020 18:47

$V = 8\sqrt{15}$

Объяснение:

(Смотри вложение)

Формула объёма пирамиды: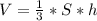 $V = \frac{1}{3}*S*h$ , где:

S - площадь основания

h - высота пирамиды

Т.к. пирамида правильная ⇒ в основании лежит правильный многоугольник, то есть, в нашем случае, равносторонний треугольник

Формула площади треугольника: SΔ =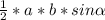 $\frac{1}{2} * a * b * sin\alpha$ , где

а - одна сторона

b - соседняя с а сторона

sin α - синус угла между сторонами a и b

Т.к. в основании треугольник равносторонний⇒все углы = 60° и a=b

SΔ =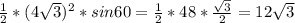 $\frac{1}{2} * (4\sqrt{3})^{2} * sin 60 = \frac{1}{2} * 48 * \frac{\sqrt{3} }{2} = 12\sqrt{3}$

Рассмотрим ΔABC

Т.к. все треугольники равносторонние (т.к. пирамида правильная) ⇒ высота AD является также медианой и биссектрисой. Получается ∠ABC =∠ACB = 60° : 2 = 30° и BD=DC = 4√3 : 2 = 2√3

Рассмотрим ΔADC

По т. Пифагора

AD = √AB²-BD²

AD = √(4√3)²-(2√3)² = √48 - 12 = √36 = 6

Высота пирамиды опускается в точку пересечения биссектрис основания, поэтому HD =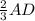 $\frac{2}{3} AD$ = 4 (Т.к. биссектрисы в точке пересечения делятся 1:2 считая от вершины)