Т.к. противолежащие ребра равны, получается AB=CD=1, AA1=DD1=2. По теореме Пифагора: AD1=√(1²+2²)=√5. Аналогично СD1=√5. AC=√(1²+1²)=√2. Рассмотрим ΔACD1: Он равнобедренный, т.к. AD1=CD1=√5. Соответственно , высота этого треугольника (назовем её D1M), проведенная к основанию АС и будет являться искомым расстоянием от точки D1. В равнобедренном треугольнике высота, проведенная к основанию, является и медианой, поэтому AM=CM=(√2)/2. Теперь по т. Пифагора можно найти катет D1M ΔD1MA: D1M=√(AD1²-AM²)=√((√5)²-((√2)/2)²)=√(5-1/2)=√4.5
Целочисленный прямоугольный треугольник, это так называемая "пифагорова тройка" : a,b,c ∈ N, для которой выполняется равенство: a² + b² = c²
Согласно формуле Евклида, для любой пары натуральных чисел m и n (m>n) целые числа: являются пифагоровой тройкой. Причём, для примитивных троек разность m-n - нечетная.
Итак, гипотенуза равна 2018 = 2 · 1009. Так как 1009 - простое число, то пусть с = 1009
Так как c = m² + n², то для числа 1009 нужно подобрать сумму квадратов.
Объяснение:
Т.к. противолежащие ребра равны, получается AB=CD=1, AA1=DD1=2. По теореме Пифагора: AD1=√(1²+2²)=√5. Аналогично СD1=√5. AC=√(1²+1²)=√2. Рассмотрим ΔACD1: Он равнобедренный, т.к. AD1=CD1=√5. Соответственно , высота этого треугольника (назовем её D1M), проведенная к основанию АС и будет являться искомым расстоянием от точки D1. В равнобедренном треугольнике высота, проведенная к основанию, является и медианой, поэтому AM=CM=(√2)/2. Теперь по т. Пифагора можно найти катет D1M ΔD1MA: D1M=√(AD1²-AM²)=√((√5)²-((√2)/2)²)=√(5-1/2)=√4.5
Целочисленный прямоугольный треугольник, это так называемая "пифагорова тройка" : a,b,c ∈ N, для которой выполняется равенство: a² + b² = c²
Согласно формуле Евклида, для любой пары натуральных чисел m и n (m>n) целые числа: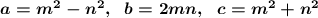
являются пифагоровой тройкой. Причём, для примитивных троек разность m-n - нечетная.
Итак, гипотенуза равна 2018 = 2 · 1009. Так как 1009 - простое число, то пусть с = 1009
Так как c = m² + n², то для числа 1009 нужно подобрать сумму квадратов.
1009 = 31² + 48 = 30² + 109 = 29² + 168 - не подходят
1009 = 28² + 15² ⇒ m = 28; n = 15
Тогда a = m² - n² = 28² - 15² = 559; b = 2mn = 2·28·15 = 840
Числа 559, 840 и 1009 - пифагорова тройка.
Но в условии число 2018 вдвое больше числа 1009, значит искомая тройка 2·559; 2·840; 2·1009
Прямоугольный треугольник имеет стороны 1118, 1680, 2018 см
Проверка : 1118² + 1680² = 2018²
1 249 924 + 2 822 400 = 4 072 324
4 072 324 = 4 072 324
ответ: 1118 см, 1680 см, 2018 см