геометрия 7-й класс!! очень Задание :Найти острые углы прямоугольного треугольника, если один из них в 4 раза больше другой. (ответ записать числами без единиц измерения через запятую, сначала меньший угол)​

Объяснение:

В-3

1

Х||у, т. к сумма внешних односторонних углов равна 180 градусов :

132+48=180 градусов

ответ : х||у

2

Тр-к РОR и тр-к SOT

PO=SO - по условию

ТО=RO - по условию

<РОR= <SOT - как вертикальные

Тр-ки равны по 2 сторонам и углу между ними, значит соответствующие элементы равны :

<ТSO=<RPO - как накрест лежащие при

РR||TS и секущей РS

<PRO=<STO - как накрест лежащие при

РТ||RS и секущей ТR

ответ : PR||TS ; PT||RS

3

Тр-к САВ - равнобедренный (АС=АВ), значит

<АВС=<АСВ

<ВСD=<ABD - как накрест лежащие при параллельных АВ и СD и секущей СВ, значит

АВ||СD

ответ : АВ||СD

32 ед².

Объяснение:

Дано: ABCDA₁B₁C₁D₁ - прямоугольный параллелепипед.

F∈AA₁, A₁F:FA = 3:4

BC = 4; AB = 2√7; AA₁=14.

Через точки F, B₁,C₁ проходит сечение.

Найти: площадь сечения.

Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.Противоположные грани параллелепипеда параллельны.

⇒ сечение FB₁C₁C - прямоугольник.

Площадь прямоугольника равна произведению смежный сторон.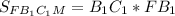

⇒

1. Пусть А₁F = 3x, тогда AF = 4x, а АА₁ = 7х = 14

7х = 14 ⇒ х = 2

Тогда A₁F = 3x = 6

2. Рассмотрим ΔFA₁B₁ - прямоугольный.

A₁F = 6; A₁B₁ = AB = 2√7;

По теореме Пифагора найдем FB₁:

Теперь найдем площадь сечения:

(ед.²)