Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их и
Проведём диагональ в квадрате и диагональ в квадрате
Рассмотрим .
У квадрата все углы прямые.
, по свойству квадрата.
, так как диагонали квадрата делят углы пополам.
по 1 признаку подобия треугольников.
4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Эту задачу можно решить двумя
1) геометрическим,,
2) векторным.
1) Проведём сечение АА1М.
Отрезок А1М как медиана и высота правильного треугольника равен:
А1М = 2√3*cos 30° = 2√3*(√3/2) = 3. Тогда А1Т = 3/2 = 1,5.
Угол между плоскостью ВСТ и прямой АТ - это угол между АТ и её проекцией на плоскость ВСТ.
Проекция АТ лежит на линии пересечения плоскостей ВСТ и АА1М.
Это линия ТР. Точка Р лежит на стороне ВС в её середине.
Отрезки АТ и ТР равны.
Искомый угол АТР равен 2arc tg (3/2)/5 = 2arc tg (3/10) = 0,5829 радиан = 33,3985°.
2) Поместим призму ребром АВ по оси Оу, точка А - начало координат. Ребро АА1 по оси Oz.
В(0; 2√3; 0), С(3; √3; 0), Т(0,75; 3√3/4; 5), А(0; 0; 0).
Уравнение плоскости ВСТ по трём точкам определяем так:
Пусть (х1, х2, х3), (у1, у2, у3) и (z1, z2, z3) – координаты первой, второй и третьей точки соответственно. Уравнение получаем из выражения: (x-x1)*(у2-y1)*(z3-z1) – (x-x1)*(z2-z1)*(y3-y1) – (y-y1)*(x2-x1)*(z3-z1) + (y-y1)*(z2-z1)*(x3-x1) + (z-z1)*(x2-x1)*(y3-y1) – (z-z1)*(y2-y1)*(x3-x1) = 0.
Подставив координаты точек, находим уравнение плоскости ВСТ:
x + √3y + 0,6z - 6 = 0.
Вектор АТ равен координатам точи Т: АТ(0,75; 3√3/4; 5).
Синус угла между прямой и плоскостью равен:
sin α = |1*0.75+√3*(3√3/4)+0*5|/(√(1²+(√3)²+0,6²)*√(0.75²+(3√3/4)²+5²)) =
= 0,550459.
Угол равен 0,5829 радиан или 33,3985 градуса.
Всё в разделе "Объяснение".
Объяснение:1. Неверно.
Два треугольника называются подобными , если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.2. Верно.
Это 2 признак подобия треугольников.
3. Верно.
Даны два квадрата. Назовём их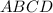 и
и 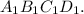
Проведём диагональ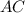 в квадрате
в квадрате 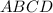 и диагональ
и диагональ 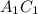 в квадрате
в квадрате 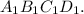
Рассмотрим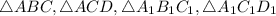 .
.
У квадрата все углы прямые.4. Неверно.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.