Геометрия 8 класс. Очень нужно.

#1. Точка С - середина отрезка АВ. Найдите координаты точки В, если C(-4:5) A(-6:-7) 2. а) ( ) AB - диаметр окружности с центром О. Найдите координаты центра

#2. окружности если А(3,7) и В (5; -1) b) [ ] Запишите уравнение окружности, используя условия пункта а)

#3. Выполните построение выясните взаимное расположение двух окружностей, заданных уравнений (х-5)? + (-3)² = 4 * (x-2)²+(y + 1)³ = 9

#4. Точки А(-6:3) ( 2:3) C(4:3) D(-6;-3) - вершины прямоугольной
трапеции с основаниями AB и CD Найдите длину средней линии и площадь трапеции.

Теоремы (свойства параллелограмма):

В параллелограмме противоположные стороны равны и противоположные углы равны: AB = CD, BC = AD, \angle ABC = \angle

ADC,\angle BAD = \angle BCD.

Диагонали параллелограмма точкой пересечения делятся пополам: AO

= OC, OB = OD.

Углы, прилежащие к любой стороне, в сумме равны 180^\circ .

Диагонали параллелограмма делят его на два равных треугольника.

Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон: AC^2 + BD^2 = 2AB^2 + 2BC^2 .

Признаки параллелограмма:

Если противоположные стороны четырехугольника попарно параллельны, то этот четырехугольник — параллелограмм.

Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.

Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм.

Если в четырехугольнике диагонали, пересекаясь, точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.

Середины сторон произвольного (в том числе невыпуклого или пространственного) четырехугольника K,\;L,\;M,\;N являются вершинами параллелограмма Вариньона.

ответ: 1) 6.

2) 30°; 150°; 30° и 150°.

3) 300.

Объяснение: 1) S=ah

72=12h

h=72:12

h=6 (см.).

2) (Начерти ромб).

Ромб-это параллелограмм, у которого все стороны равны. Значит, формула нахождения площади, как у параллелограмма.

S=ah

98=7a

a=98:7

a=14.

Я уже говорила, что ромб-это параллелограмм, у которого все стороны равны. Значит, а=b=с=d=14.

Проведя высоту, можно заметить, что в образованном треугольнике гипотенуза больше катета в 2 раза. Следовательно, работает следующее правило: против ∠ в 30° лежит катет, равный половине гипотенузы. Значит, острый ∠ ромба=30°.

Тупой ∠ ромба=180°-30°=150°.

В ромбе противоположные углы равны⇒∠1=∠3=30°, ∠2=∠4=150°.

3) (Начерти трапецию).

Проведём высоту ВН и рассмотрим получившийся треугольник-прямоугольный, так как ВН-высота.

Острый угол трапеции равен 45°, а значит и острый угол получившегося треугольника равен 45°. Найдём оставшийся неизвестный угол треугольника. 90°-45°=45°. Острые углы прямоугольного треугольника равны, значит, треугольник равнобедренный⇒катет а=катету в (или высоте h).

a=h=(40-20):2=20:2=10.

S=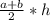

S=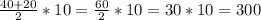.