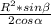Геометрия 8класс 4токсан тжб ​

Тебе дан равнобедренный треугольник, у равнобедренного треугольника 1 боковая сторона = второй, боковая сторона ас=12 см, значит св=12. Почему св= 12? Так как угол С 120 градусов, значит он больше 90 и его нужно указать вверху треугольника. Далее проводишь биссектрису CH. Чтобы найти биссектрису должен(а) записать соотношение AC/CH=CH/CB и выражаешь CH(так как записана 2 раза то у тебя получается квадрат биссектрисы). CH(в квадрате)=ас*св= 12*12=144 см(это бисстектр в квадрате) CH=12 см
Так как CH биссектриса, то она делит угол на 2 равные части, то есть 120:2=60. 
Мы знаем, что биссектриса образовывает угол в 90 градусов, угол H= 90, найдем угол А. Сумма углов треугольника = 180, чтобы найти угол А надо из 180 вычесть 90 и 60= 30 градусам. Катет лежащий против угла в 30 градусов равен половине гипотенузы CH= 12:2 = 6 см

Через вершину конуса проведена плоскость под углом альфа к плоскости основания. Эта плоскость пересекает основание конуса по морде, которая видна из центра его основания под углом бета. Радиус основания R. Найдите площадь сечения.

Объяснение:

Образующие конуса равны , поэтому ΔABS равнобедренный. Пусть SK⊥AB, тогда ОК⊥АВ по т. О трех перпендикулярах.Т.к. ОА=ОВ как радиусы, то высота КО является биссектрисой ∠АОК=.

ΔАОК- прямоугольный ,

cos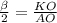 , KO=R*cos;

sin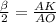 ,AK=R*sin ,AB=α2Rsin .

ΔSKO прямоугольный ,cos α=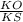, KS=R*cos/cosα.

S=0,5*AB*SK ,S=0,5*2R*sin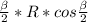/ cosα,

S=0,5*R²*sinβ/cosα=