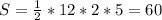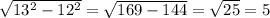Геометрия 8сынып 125 бет 1,2,3 есептерінің жауабын беріңіздерш

Если угол при основании 45 градусов, то прямоугольный треугольник, где высота трапеции стороной этого треугольника, а бедро трапеции гипотенузой - равнобедренный, так как второй угол этого прямоугольного треугольника тоже 90-45=45 градусов. Значит, кусочек нижнего основания трапеции, отсекаемый ее высотой равен тоже 3 см. Проведем вторую высоту трапеции, тогда получим, что высоты делят большое основание на три части - две по 3 см и одна - как малое основание 5 см. Следовательно, большое основание имеет размер 3+5+3=11 см.

Найдём, по теореме Пифагора, второй катет в данном прямоугольном треугольнике, он равен , найденный нами катет является меньшим, поэтому вращение треугольника происходит вокруг него, при этом образуется конус. Осевое сечение конуса представляет собой равнобедренный треугольник, в котором боковые стороны равны образующей, а основание равно диаметру окружности, лежащей в основании конуса, в данном случае образующая равна гипотенузе, диаметр-двум большим катетам данного треугольника, а высота-меньшему катету, значит площадь сечения равна: