Пусть ABC' — произвольный треугольник. Проведем через вершину B прямую, параллельную прямой AC. Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны прямой BC.Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD. Поэтому сумма углов треугольника при вершинах B и С равна углу ABD.Сумма всех трех углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB, то их сумма равна 180°. Теорема доказана.
Точки М i Р лежать відповідно на сторонах АB i BC трикутника АВС, АВ* РВ=СB*МB. Доведіть, що МР паралельна АC.
Объяснение:
АВ* РВ=СB*МB /: СВ*РВ ,
, .
По второму признаку подобия : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника ( ) и углы , заключённые между пропорциональными сторонами, равны ( ∠В-общий) , то такие треугольники подобны⇒ соответственные углы равны : ∠ВМР=∠ВАС. Но эти углы по расположению соответственные при секущей АВ. Значит по признаку параллельности прямых МР║АС
Точки М i Р лежать відповідно на сторонах АB i BC трикутника АВС, АВ* РВ=СB*МB. Доведіть, що МР паралельна АC.
Объяснение:
АВ* РВ=СB*МB /: СВ*РВ ,
По второму признаку подобия : если две стороны одного треугольника пропорциональны двум сторонам другого треугольника (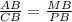
) и углы , заключённые между пропорциональными сторонами, равны ( ∠В-общий) , то такие треугольники подобны⇒ соответственные углы равны : ∠ВМР=∠ВАС. Но эти углы по расположению соответственные при секущей АВ. Значит по признаку параллельности прямых МР║АС