Через точку А, лежащую на окружности радиусом 10см с центром в точке О. проведена касательная АМ . Отрезок ОМ пересекает окружность в точке В. Найти градусную меру меньшей из дуг АВ, если АМ =10см.
а) Радиус окружности, описанной около правильного треугольника:
R = a√3/3
C = 2πa√3/3
б) Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, и гипотенуза является диаметром окружности. Гипотенузу найдем по теореме Пифагора:
с = √(a² + b²)
C = πd = π√(a² + b²)
в) Проведем высоту к основанию равнобедренного треугольника. Она является так же медианой. Из образовавшегося прямоугольного треугольника выразим косинус угла при основании:
cosα = (a/2) / b = a / (2b).
Из основного тригонометрического тождества получим:
sinα = √(1 - cos²α) = √(1 - a²/(4b²)) =
Радиус окружности, описанной около любого треугольника, равен отношению стороны к удвоенному синусу противолежащего угла:
R = b/(2sinα)
г) Центр окружности, описанной около прямоугольника, лежит в точке пересечения диагоналей. Радиус ее равен половине диагонали.
Из треугольника, образованного меньшей стороной и двумя половинами диагоналей по теореме косинусов:
a² = R² + R² - 2R·R·cosα = R²(2 - 2cosα)
R² = a² / (2 - 2cosα)
R = a / √(2 - 2cosα)
C = 2πa / √(2 - 2cosα)
д) Правильный шестиугольник делится диагоналями, проведенными через центр, на шесть равных равносторонних треугольников. Тогда площадь одного треугольника:
S = 24√3 / 6 = 4√3 см²
S = a²√3 / 4, где а - сторона треугольника.
a = √(4S / √3) = √(4 · 4√3 / √3) = 4 см
Сторона шестиугольника равна радиусу описанной окружности, тогда
а) Радиус окружности, описанной около правильного треугольника:
R = a√3/3
C = 2πa√3/3
б) Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, и гипотенуза является диаметром окружности. Гипотенузу найдем по теореме Пифагора:
с = √(a² + b²)
C = πd = π√(a² + b²)
в) Проведем высоту к основанию равнобедренного треугольника. Она является так же медианой. Из образовавшегося прямоугольного треугольника выразим косинус угла при основании:
cosα = (a/2) / b = a / (2b).
Из основного тригонометрического тождества получим:
sinα = √(1 - cos²α) = √(1 - a²/(4b²)) =
Радиус окружности, описанной около любого треугольника, равен отношению стороны к удвоенному синусу противолежащего угла:
R = b/(2sinα)
г) Центр окружности, описанной около прямоугольника, лежит в точке пересечения диагоналей. Радиус ее равен половине диагонали.
Из треугольника, образованного меньшей стороной и двумя половинами диагоналей по теореме косинусов:
a² = R² + R² - 2R·R·cosα = R²(2 - 2cosα)
R² = a² / (2 - 2cosα)
R = a / √(2 - 2cosα)
C = 2πa / √(2 - 2cosα)
д) Правильный шестиугольник делится диагоналями, проведенными через центр, на шесть равных равносторонних треугольников. Тогда площадь одного треугольника:
S = 24√3 / 6 = 4√3 см²
S = a²√3 / 4, где а - сторона треугольника.
a = √(4S / √3) = √(4 · 4√3 / √3) = 4 см
Сторона шестиугольника равна радиусу описанной окружности, тогда
Длина окружности вычисляется по формуле:
С = 2πR или C = πd
где R - радиус окружности,
d - диаметр окружности.
а) Радиус окружности, описанной около правильного треугольника:
R = a√3/3
C = 2πa√3/3
б) Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, и гипотенуза является диаметром окружности. Гипотенузу найдем по теореме Пифагора:
с = √(a² + b²)
C = πd = π√(a² + b²)
в) Проведем высоту к основанию равнобедренного треугольника. Она является так же медианой. Из образовавшегося прямоугольного треугольника выразим косинус угла при основании:
cosα = (a/2) / b = a / (2b).
Из основного тригонометрического тождества получим:
sinα = √(1 - cos²α) = √(1 - a²/(4b²)) =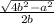
Радиус окружности, описанной около любого треугольника, равен отношению стороны к удвоенному синусу противолежащего угла:
R = b/(2sinα)
г) Центр окружности, описанной около прямоугольника, лежит в точке пересечения диагоналей. Радиус ее равен половине диагонали.
Из треугольника, образованного меньшей стороной и двумя половинами диагоналей по теореме косинусов:
a² = R² + R² - 2R·R·cosα = R²(2 - 2cosα)
R² = a² / (2 - 2cosα)
R = a / √(2 - 2cosα)
C = 2πa / √(2 - 2cosα)
д) Правильный шестиугольник делится диагоналями, проведенными через центр, на шесть равных равносторонних треугольников. Тогда площадь одного треугольника:
S = 24√3 / 6 = 4√3 см²
S = a²√3 / 4, где а - сторона треугольника.
a = √(4S / √3) = √(4 · 4√3 / √3) = 4 см
Сторона шестиугольника равна радиусу описанной окружности, тогда
R = a = 4 см
С = 2π · 4 = 8π см
Длина окружности вычисляется по формуле:
С = 2πR или C = πd
где R - радиус окружности,
d - диаметр окружности.
а) Радиус окружности, описанной около правильного треугольника:
R = a√3/3
C = 2πa√3/3
б) Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, и гипотенуза является диаметром окружности. Гипотенузу найдем по теореме Пифагора:
с = √(a² + b²)
C = πd = π√(a² + b²)
в) Проведем высоту к основанию равнобедренного треугольника. Она является так же медианой. Из образовавшегося прямоугольного треугольника выразим косинус угла при основании:
cosα = (a/2) / b = a / (2b).
Из основного тригонометрического тождества получим:
sinα = √(1 - cos²α) = √(1 - a²/(4b²)) =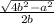
Радиус окружности, описанной около любого треугольника, равен отношению стороны к удвоенному синусу противолежащего угла:
R = b/(2sinα)
г) Центр окружности, описанной около прямоугольника, лежит в точке пересечения диагоналей. Радиус ее равен половине диагонали.
Из треугольника, образованного меньшей стороной и двумя половинами диагоналей по теореме косинусов:
a² = R² + R² - 2R·R·cosα = R²(2 - 2cosα)
R² = a² / (2 - 2cosα)
R = a / √(2 - 2cosα)
C = 2πa / √(2 - 2cosα)
д) Правильный шестиугольник делится диагоналями, проведенными через центр, на шесть равных равносторонних треугольников. Тогда площадь одного треугольника:
S = 24√3 / 6 = 4√3 см²
S = a²√3 / 4, где а - сторона треугольника.
a = √(4S / √3) = √(4 · 4√3 / √3) = 4 см
Сторона шестиугольника равна радиусу описанной окружности, тогда
R = a = 4 см
С = 2π · 4 = 8π см