1. Сумма внутренних углов треугольника равна 180°. Тогда третий угол равен 180°-93°-48°=39°. ответ:39° 2. Сумма острых углов прямоугольного треугольника равна 90°. Тогда Х+4Х=90°. => Х=18°, второй угол = 72°. ответ: 18° и 72°. 3. Внешние углы треугольнмкя являются смежными углами с внутренними углами и в сумме равны 180°.Значит два внутренних угла треугольника равны 180°-104°=76° и 180°-124°=56°. Третий угол равен 180°-76°-56°=48° ответ: углы треугольника равны 56°, 76° и 48°. 4. <ABM=45°, так как ВМ - биссектриса прямого угла. <ABH=<ABM-<HBM = 45°-12°=33°. <A=90°-33°=57°. <C=90-57=33°. 5. Пусть угол при основании равен Х°, тогда угол, противолежащий основанию, равен Х-24°. Сумма внутренних углов треугольника равна 180°, тогда Х+Х+(X-24)=180 => 3X=204 и Х=68°. Угол против основания равен 180°-2*68° = 44°. ответ: углы треугольника равны 68°, 68° и 44°. 6. ВН=6√3см, так как ВН=tg60*AH, tg60=√3. Или по Пифагору: ВН=√(12²-6²)=6√3, так как <ABH=30° и АВ=2*АН. ВН²=АН*НС (свойство высоты из прямого угла). Тогда 108=6*НС => НС=18см. ответ: НС=18 см.
Т.к. все три точки сечения призмы лежат попарно в одних и тех же плоскостях, то сечение строится попарным соединением точек - получаем в сечении ΔAB1C
Т.к. четырехугольники AA1B1B и BB1C1C равны, то равны и их диагонали AB1 и B1C ⇒ ΔAB1C равнобедренный.
Проведем медиану B1O в ΔAB1C, одновременно она будет и высотой ⇒ B1O ⊥ AC
Проведем медиану BO в равнобедренном ΔABC, одновременно она будет и высотой ⇒ BO ⊥ AC
Значит BOB1 будет углом между плоскостью сечения и нижним основанием, а т.к. нижнее и верхнее основание параллельны, то он равен углу между плоскостью сечения и верхним основанием, т.е. 45°
Из ΔBOB1, зная, что BO равно половине диагонали квадрата, найдем, что высота призмы BB1 = d /2
Из прямоугольного равнобедренного ΔABC с гипотенузой AC = d, найдем
Объем призмы найдем как произведение площади основания на высоту:
третий угол равен 180°-93°-48°=39°.
ответ:39°
2. Сумма острых углов прямоугольного треугольника равна 90°.
Тогда Х+4Х=90°. => Х=18°, второй угол = 72°.
ответ: 18° и 72°.
3. Внешние углы треугольнмкя являются смежными углами с внутренними углами и в сумме равны 180°.Значит два внутренних угла треугольника равны 180°-104°=76° и 180°-124°=56°.
Третий угол равен 180°-76°-56°=48°
ответ: углы треугольника равны 56°, 76° и 48°.
4. <ABM=45°, так как ВМ - биссектриса прямого угла.
<ABH=<ABM-<HBM = 45°-12°=33°.
<A=90°-33°=57°. <C=90-57=33°.
5. Пусть угол при основании равен Х°,
тогда угол, противолежащий основанию, равен Х-24°.
Сумма внутренних углов треугольника равна 180°, тогда
Х+Х+(X-24)=180 => 3X=204 и Х=68°. Угол против основания равен
180°-2*68° = 44°.
ответ: углы треугольника равны 68°, 68° и 44°.
6. ВН=6√3см, так как ВН=tg60*AH, tg60=√3.
Или по Пифагору:
ВН=√(12²-6²)=6√3, так как <ABH=30° и АВ=2*АН.
ВН²=АН*НС (свойство высоты из прямого угла). Тогда
108=6*НС => НС=18см.
ответ: НС=18 см.
Т.к. все три точки сечения призмы лежат попарно в одних и тех же плоскостях, то сечение строится попарным соединением точек - получаем в сечении ΔAB1C
Т.к. четырехугольники AA1B1B и BB1C1C равны, то равны и их диагонали AB1 и B1C ⇒ ΔAB1C равнобедренный.
Проведем медиану B1O в ΔAB1C, одновременно она будет и высотой ⇒ B1O ⊥ AC
Проведем медиану BO в равнобедренном ΔABC, одновременно она будет и высотой ⇒ BO ⊥ AC
Значит BOB1 будет углом между плоскостью сечения и нижним основанием, а т.к. нижнее и верхнее основание параллельны, то он равен углу между плоскостью сечения и верхним основанием, т.е. 45°
Из ΔBOB1, зная, что BO равно половине диагонали квадрата, найдем, что высота призмы BB1 = d /2
Из прямоугольного равнобедренного ΔABC с гипотенузой AC = d, найдем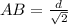
Объем призмы найдем как произведение площади основания на высоту: