ответ: Не верьте громоздким готовым формулам, они отучают думать
Объяснение:
Трапеции бывают разные. Вот если мы применим рисунок со стандартной трапецией, то выяснится, что она не существует.
неизвестная будет отрицательная и прочие неприятности. Но на втором рисунке тоже трапеция, так как АД||ВС, а две другие стороны не параллельны. Вот его мы и решим.
Когда мы провели две высоты мы от основания отрезали отрезок
что у = АД - 8+х или у=4+х Это первое уравнение.
Из прямоугольных треугольников на рисунке выразим высоту, не спеша вдумчиво и применяя теорему святого Пифагора:
Из ВНА будет h² = AB² - x²
Из СМД будет h² = CД² - у² и так как левые части равны, приравняем и правые части АВ²-х² = СД² -у² или подставив значения боковых сторон 14²-х² = 15²-у² а отсюда уже
у²-x²=225-196 = 29 уравнение. Решив систему этих уравнений (я расписывать это здесь не буду, нудно) мы получим, что х=
2)Трикутники АВВ1 і АСС1 подібні за трьома кутами ( два при паралельних прямих і третій А спільний) отже
АС/АВ=СС1/ВВ1=11/(9+11) звідси
ВВ1=20*СС1/11=20*8,1/11=162/11
3)Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость.
В нашем случае проекциями данного нам отрезка на плоскости - это отрезки, соединяющие концы данного отрезка на плоскости и перпендикуляра, опущенного на данную плоскость.Но плоскости перпендикулярны, значит эти перпендикуляры - это расстояния от концов отрезка до линии пересечения плоскостей. То есть проекцией отрезка АВ на плоскость α будет отрезок АВ1,а углом между отрезком АВ и плоскостью α будет угол ВАВ1. Соответственно проекцией отрезка АВ на плоскость β будет отрезок ВА1,а углом между отрезком АВ и плоскостью β будет угол АВА1.
Синус угла ВАВ1 равен отношению противолежащего катета ВВ1 к гипотенузе AB, то есть Sin(ВАВ1)=12/24=1/2. Значит угол между отрезком АВ и плоскостью α равен 30°.
Синус угла АВА1 равен отношению противолежащего катета АА1 к гипотенузе AB, то есть Sin(АВА1)=12√2/24=√2/2. Значит угол между отрезком АВ и плоскостью α равен 45°.
ответ: Углы, образованные отрезком с плоскостями равны 30° и 45°.
4)находим высоту, проведенную к стороне 14
она равна 12( можно найти через формулу Герона площадь, а затем поделить на половину стороны 14см)
ну а дальше расстояние равно гипотенузе с катетами 12 и 16 и равна 20см
5)1. Проведем перпендикуляры из точек С и Д на АВ. Обозначим их СК и ДКПо условию
угол СКД=45.
2. Из треуг. АВС СК - высота правильного треугольника
СК=АВ*sqrt {3}/2=6
3. В треуг. АВД ДК - высота, опущенная на основание равнобедренного треугольника. Как известно, она совпадает с медианой.
АК= АВ/2= 2sqrt {3}
Из прямоуг. трег. АКД по теореме Пифагора
ДК= sqrt ( АД^2-АК^2)= sqrt( 14-12)= sqrt2
4 В треугольнике СКД СК=6, СД=sqrt2 . Угол СКД= 45
ответ: Не верьте громоздким готовым формулам, они отучают думать
Объяснение:
Трапеции бывают разные. Вот если мы применим рисунок со стандартной трапецией, то выяснится, что она не существует.
неизвестная будет отрицательная и прочие неприятности. Но на втором рисунке тоже трапеция, так как АД||ВС, а две другие стороны не параллельны. Вот его мы и решим.
Когда мы провели две высоты мы от основания отрезали отрезок
что у = АД - 8+х или у=4+х Это первое уравнение.
Из прямоугольных треугольников на рисунке выразим высоту, не спеша вдумчиво и применяя теорему святого Пифагора:
Из ВНА будет h² = AB² - x²
Из СМД будет h² = CД² - у² и так как левые части равны, приравняем и правые части АВ²-х² = СД² -у² или подставив значения боковых сторон 14²-х² = 15²-у² а отсюда уже
у²-x²=225-196 = 29 уравнение. Решив систему этих уравнений (я расписывать это здесь не буду, нудно) мы получим, что х=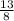
Тогда из треугольника ВНС
h² = 14² -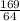
= 13,9
И это решение верное.
1)г
2)Трикутники АВВ1 і АСС1 подібні за трьома кутами ( два при паралельних прямих і третій А спільний) отже
АС/АВ=СС1/ВВ1=11/(9+11) звідси
ВВ1=20*СС1/11=20*8,1/11=162/11
3)Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость.
В нашем случае проекциями данного нам отрезка на плоскости - это отрезки, соединяющие концы данного отрезка на плоскости и перпендикуляра, опущенного на данную плоскость.Но плоскости перпендикулярны, значит эти перпендикуляры - это расстояния от концов отрезка до линии пересечения плоскостей. То есть проекцией отрезка АВ на плоскость α будет отрезок АВ1,а углом между отрезком АВ и плоскостью α будет угол ВАВ1. Соответственно проекцией отрезка АВ на плоскость β будет отрезок ВА1,а углом между отрезком АВ и плоскостью β будет угол АВА1.
Синус угла ВАВ1 равен отношению противолежащего катета ВВ1 к гипотенузе AB, то есть Sin(ВАВ1)=12/24=1/2. Значит угол между отрезком АВ и плоскостью α равен 30°.
Синус угла АВА1 равен отношению противолежащего катета АА1 к гипотенузе AB, то есть Sin(АВА1)=12√2/24=√2/2. Значит угол между отрезком АВ и плоскостью α равен 45°.
ответ: Углы, образованные отрезком с плоскостями равны 30° и 45°.
4)находим высоту, проведенную к стороне 14
она равна 12( можно найти через формулу Герона площадь, а затем поделить на половину стороны 14см)
ну а дальше расстояние равно гипотенузе с катетами 12 и 16 и равна 20см
5)1. Проведем перпендикуляры из точек С и Д на АВ. Обозначим их СК и ДКПо условию
угол СКД=45.
2. Из треуг. АВС СК - высота правильного треугольника
СК=АВ*sqrt {3}/2=6
3. В треуг. АВД ДК - высота, опущенная на основание равнобедренного треугольника. Как известно, она совпадает с медианой.
АК= АВ/2= 2sqrt {3}
Из прямоуг. трег. АКД по теореме Пифагора
ДК= sqrt ( АД^2-АК^2)= sqrt( 14-12)= sqrt2
4 В треугольнике СКД СК=6, СД=sqrt2 . Угол СКД= 45
По теореме косинусов
СД^2=36+2-2*6*sqrt2*сos 45=26
СД=корень из 26
Объяснение: