Пусть точка P(x₀, y₀) удовлетворяет системе уравнений. Возьмём квадратный корень из левой и правой части каждого уравнения:
Первое уравнение задаёт расстояние от точки P(x₀, y₀) до точки A(-4, -3), равное трём. Второе уравнение задаёт расстояние от точки P(x₀, y₀) до точки B(-1, 1), равное двум.
Заметим, что расстояние между точками A(-4, -3) и B(-1, 1) равно . Расстояние между данными точками равно сумме расстояний между точками P(x₀, y₀) и A(-4, -3) и между точками P(x₀, y₀) и B(-1, 1) (AB (5) = AP (3) + PB (2)). Значит, точка P(x₀, y₀) находится на отрезке между точками A(-4, -3) и B(-1, 1) и делит его в отношении 3 : 2, считая от точки A(-4, -3). Тогда справедливо
Поскольку точка A находится не в начале координат, выполнив параллельный перенос на вектор , мы получим координаты точки P(x₀, y₀): .
Раз она равнобедренная, то и углы равны у ее бедер - по 45 градусов.
Вот и все. Теперь рисуйте трапецию, опускайте вертикальные (поперек нижнего основания) прямые из крайних точек верхнего основания. Так получатся два равных треугольника прямоугольных. В них угол при гиотенузе 45 градусов, значит они равнобеюренные. Один катет является высотой трапеции, а второй катет половине разницы длин оснований трапеции. Значит, высота ее равна 14 см.
т.е. рисуем трапецию АВСД, где основания АВ=24см и СД=52см, угол С= углу Д=45 градусов. Проводим перпендикуляры на СД из А и В. Точки пересечения называем, соответственно Е и К. Треугольники АЕД и ВКС прямоугольные, равнобедренные и равные. Смотрим один из них, АЕД.
Тут катет АЕ= высота трапеции АВСД, катет ЕД = (СД-АВ)/2
(-2,2; -0,6)
Объяснение:
Пусть точка P(x₀, y₀) удовлетворяет системе уравнений. Возьмём квадратный корень из левой и правой части каждого уравнения:
Первое уравнение задаёт расстояние от точки P(x₀, y₀) до точки A(-4, -3), равное трём. Второе уравнение задаёт расстояние от точки P(x₀, y₀) до точки B(-1, 1), равное двум.
Заметим, что расстояние между точками A(-4, -3) и B(-1, 1) равно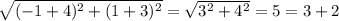
. Расстояние между данными точками равно сумме расстояний между точками P(x₀, y₀) и A(-4, -3) и между точками P(x₀, y₀) и B(-1, 1) (AB (5) = AP (3) + PB (2)). Значит, точка P(x₀, y₀) находится на отрезке между точками A(-4, -3) и B(-1, 1) и делит его в отношении 3 : 2, считая от точки A(-4, -3). Тогда справедливо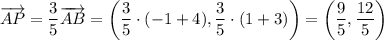 
Поскольку точка A находится не в начале координат, выполнив параллельный перенос на вектор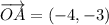
, мы получим координаты точки P(x₀, y₀): 
.
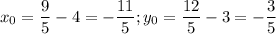Решением системы является точка (-2,2; -0,6).
Да чего ту сложного-то?
Глядите:
Раз она равнобедренная, то и углы равны у ее бедер - по 45 градусов.
Вот и все. Теперь рисуйте трапецию, опускайте вертикальные (поперек нижнего основания) прямые из крайних точек верхнего основания. Так получатся два равных треугольника прямоугольных. В них угол при гиотенузе 45 градусов, значит они равнобеюренные. Один катет является высотой трапеции, а второй катет половине разницы длин оснований трапеции. Значит, высота ее равна 14 см.
т.е. рисуем трапецию АВСД, где основания АВ=24см и СД=52см, угол С= углу Д=45 градусов. Проводим перпендикуляры на СД из А и В. Точки пересечения называем, соответственно Е и К. Треугольники АЕД и ВКС прямоугольные, равнобедренные и равные. Смотрим один из них, АЕД.
Тут катет АЕ= высота трапеции АВСД, катет ЕД = (СД-АВ)/2
Считаем:
АЕ=ЕД=(СД-АВ)/2=(52-24)/2=28/2=14см
Ура!)