И; Прямі AD і BC паралельні. Відрізки АВ і DC перетинаються в точці О, причому 0- середина відрізка CD. OB = 8 см, ОС =5 см, AD=9 см. Знайдіть периметр трикутника ADO.
1. Апофема L определяется по т Пифагора L²=h²+(a/2)²=100+4=104, L = = 2 ≈ 10,2 см
Объяснение:
2. Площадь основания находится как площадь равностороннего Δ с со стороной a, So = a²/4=4. Аопофема L находится из условия L²=b²-(a/2)²=64-2,25=61,75, L ≈ 7,59 cм, тогда площадь 1 Грани = aL/2 ≈ 1,5·7,59≈11,78 cм², а вся площадь боковой поверхности = утроенной площади боковой грани ≈ 33,36 см². Общая площадь = 4√3+33,36 ≈33,36+6,93 ≈ 40,29 ≈ 40 см²
3. Диагональ основания d =6, тогда высота находится из соотношения h² = b²-(d/2)²=144-18=126, h =3, площадь основания So=a²=36, объём V=Soh/3=36≈ 95,25 ≈ 95 см²
1. Апофема L определяется по т Пифагора L²=h²+(a/2)²=100+4=104, L =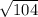
= 2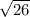
≈ 10,2 см
Объяснение:
2. Площадь основания находится как площадь равностороннего Δ с со стороной a, So =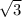
a²/4=4
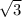. Аопофема L находится из условия L²=b²-(a/2)²=64-2,25=61,75, L ≈ 7,59 cм, тогда площадь 1 Грани = aL/2 ≈ 1,5·7,59≈11,78 cм², а вся площадь боковой поверхности = утроенной площади боковой грани ≈ 33,36 см². Общая площадь = 4√3+33,36 ≈33,36+6,93 ≈ 40,29 ≈ 40 см²
3. Диагональ основания d =6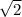
, тогда высота находится из соотношения h² = b²-(d/2)²=144-18=126, h =3
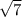, площадь основания So=a²=36, объём V=Soh/3=36
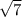≈ 95,25 ≈ 95 см²
полное условие - прикрепленное вложение.
Задание 1.
На картинке отмечены односторонние углы при прямых a и b и секущей с, в сумме они должны давать 180°.
110°+70°=180° ⇒ 180°=180° ⇒ a || b
Задание 2.
На картинке отмечены односторонние углы при прямых a и b и секущей с, в сумме они должны давать 180°.
125°+65°=180° ⇒ 190°=180° ⇒ a и b не параллельны
Задание 3.
На картинке отмечены накрест лежащие углы при прямых a и b и секущей с, они должны быть равны.
40°=40° ⇒ a || b
Задание 4.
На картинке отмечены односторонние углы при прямых a и b и секущей с, в сумме они должны давать 180°.
180°-a+a=180° ⇒ 180°=180° ⇒ a || b