Идет 13.14. Укажите нахождения расст о конкретной точке на берегу) до корабля, находящегося не- 6 далеко в море (рис. 13.8, а). Используйте рисунок 13.8, б. V. Ү:
По свойству угла между высотами параллелограмма, проведенными из тупого угла(угол между высотами параллелограмма, проведенными из тупого угла, равен острому углу параллелограмма):
Объяснение:
Так как призма прямая, то длина ее высоты равна длине бокового ребра призмы.
Площадь боковой поверхности призмы равна:
S(бок) = S(AA₁C₁C) + S(BB₁C₁C) + S(AA₁B₁B)
Найдем боковую сторону равнобедренного треугольника в основании призмы:
Проведем высоту BH равнобедренного треугольника ABC с основанием AC.
По свойству высоты равнобедренного треугольника, проведенной к основанию, BH будет медианой, поэтому AH = CH = AC/2 = 4 см
По теореме Пифагора найдем AB:
AB =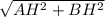 =
= 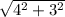 = 5
= 5
S(AA₁C₁C) = AA₁ * AC = 6 * 8 = 48 см²
S(BB₁C₁C) = BB₁ * BC = 6 * 5 = 30 см²
S(AA₁B₁B) = AB * AA₁ = 5 * 6 = 30 см²
S(бок) = 48 см² + 30 см² + 30 см² = 108 см²
< PES = 90°
< PFS = 90°
< ESF = 110°
< PTE = 70°
< PNF = 70°
< NPF = 20°
< TRE = 20°
< NPT = 110°
Объяснение:
Так как PE и PF - высоты, то
< PES = 90°
< PFS = 90°
Сумма углов четырехугольника 360°, поэтому
< PES + < EPF + < PFS + < ESF = 360°
< ESF = 360° - (< PES + < EPF + < PFS) = 360° - (90° + 70° + 90°) = 110°
По свойству угла между высотами параллелограмма, проведенными из тупого угла(угол между высотами параллелограмма, проведенными из тупого угла, равен острому углу параллелограмма):
< PTE = < PNF = < FPE = 70° - острые углы параллелограмма
< NPF = 180° - < PFN - < PNF = 180° - 90° - 70° = 20°
< TRE = 180° - <PET - < PTE = 180° - 90° - 70° = 20°
< NPT = < NPF + < FPE + < EPT = 20° + 70° + 20° = 110°