Геометрия: ИMN - epegutstareer-8 ДААСАКое тв. [ ХКс C3.

И
MN - epeguts
tareer-8 ДААС
А
Кое тв. [" ХК
с C
3.

Показать ответ

Ответ:

Joom372

04.04.2022 07:41

Даны точка P(-1;-2;2) и прямая (x/2)=(y/-2)=((z-2)/3).

Из уравнения прямой получим:

s = 2; -2; 3 - направляющий вектор прямой;

M1 = 0; 0; 2 - точка лежащая на прямой.

Находим вектор РМ1.

РM1 = {M1x - Рx; M1y - Рy; M1z - Рz} = 0 - (-1); 0 - (-2); 2 - 2 = 1; 2; 0

Площадь параллелограмма лежащего на двух векторах РM1 и s:

S = |РM1 × s|

РM1 × s = i j k

1 2 0

2 -2 3 =

= i (2·3 - 0·(-2)) - j (1·3 - 0·2) + k (1·(-2) - 2·2) =

= i (6 – 0) - j (3 – 0) + k (-2 – 4) =

= 6; -3; -6.

Зная площадь параллелограмма и длину стороны найдем высоту (расстояние от точки до прямой):

d = |РM1×s||s| = √(6² + (-3)² + (-6)²)/√(2² + (-2)² +3²) = √81/√17 = √(81/17) = 9√17/17 ≈ 2,18282.

0,0(0 оценок)

Ответ:

мая101

08.08.2022 21:55

Объяснение:

Додакове: 1) Длина основания 14п, формула для неё 2пR, где R - радиус основания. Площадь осевого сечения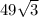 $49\sqrt3$ см^2 - это площадь прямоугольника со сторонами, равными диаметру и образующей. Найдем радиус, что будет равен 7, а диаметр в два раза больше радиуса и равен 14. Тогда найдём образующую, и она будет равна 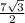$\frac{7\sqrt3}{2}$ . 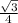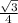Угол между диагональю и основанием равен тангенсу альфа равному отношению образующей к диаметру и равен $\frac{\sqrt{3}}{4}$ , тогда угол равен арктангенс $\frac{\sqrt3}{4}$ .

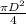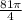
2) Так как прямоугольник вращается вокруг меньшей стороны, он описывает цилиндр с диаметром, равным меньшей стороне. Периметр сумма сторон, площадь - произведение. Тогда у нас будет a+b = 21, a*b=108, тогда меньшая сторона будет равна 9. Площадь основания $\frac{\pi D^2}{4}$ , и будет равна $\frac{81\pi }{4}$

Вариант 1: 1) Образующая это катет прямоугольного треугольника с гипотенузой - диагональю и катетом - диаметром. И она будет равна корень из 20^2-12^2 = 16. Площадь основания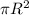 $\pi R^2$ и равна $36\pi$

2) Косинус 60 градусов = диаметр/диагональ и тогда будет 1/2 = диаметр/10 , откуда диаметр равен 5, тогда площадь основания по той же формуле будет равна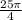 $\frac{25\pi }{4}$

3) По теореме Пифагора найдём диаметр, то есть сторону прямоугольника, и она будет равна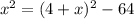 x^2=(4+x)^2-64 , откуда х = 6, диаметр, тогда площадь осевого сечения равна 6*8 = 48

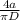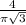4) Отношение площадей будет равно отношению $\frac{4a}{\pi D}$ , где а - образующая цилиндра. Так как вокруг осевого сечения можно описать окружность, а угол между диагоналями - центральный, то угол между диагональю и диаметром равен 30 градусам, значит a/D = тангенсу 30 градусов, равному $\frac{1}{\sqrt3}$ , тогда отношение площадей будет равно $\frac{4}{\pi \sqrt3}$ (мне кажется там ошибка в условии, дан угол не между диагоналями, а между диагональю и диаметром, если сравнить эту задачу с 4 задачей второго варианта, поэтому решение может быть неверным)