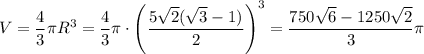Войти Регистрация Спроси ai-bota

Используя циркуль и линейку без делений, через точку М провести прямую так, чтобы она пересекала отрезок АС в его середине вот картинка

Используя циркуль и линейку без делений, через точку М провести прямую так, чтобы она пересекала отр

Показать ответ

Ответ:

olgakankova86

08.04.2021 13:17

Проведем в равнобедренном треугольнике высоту из вершины треугольника на его основание.Высота в равнобедренном треугольнике является медианой,биссектрисой>высота делит основание на 2 равные части равные 36.Рассмотрим прямоугольный треугольник нам известна гипотенуза(она же сторона равнобедренного треугольника) и основание(оно же является половиной основания равнобедренного треугольника).По теореме Пифагора найдем неизвестную часть треугольника(она же высота в равнобедренном треугольнике) высота^2=39^2-36^2,высота=15
S=(a*h(a))/2=(72*15)/2=540
ответ:540

0,0(0 оценок)

Ответ:

vikylyalol

14.02.2020 04:21

Объём шара определён формулой: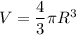 $V=\dfrac{4}{3}\pi R^3$ .

Шар можно вписать в любую правильную пирамиду. Центр шара лежит на высоте пирамиды и совпадает с центром окружности, вписанной в равнобедренный треугольник, боковой стороной которого является апофема пирамиды, а высотой - высота пирамиды. Радиус шара равен радиусу этой окружности.

Радиус шара R, высота пирамиды H и радиус окружности r, вписанной в основание пирамиды, связаны соотношением: $\dfrac{R}{H-R}=\dfrac{r}{\sqrt{H^2+r^2}}$

Радиус основания r = AD/2 = 10/2 = 5. Высота пирамиды H определим по теореме Пифагора из треугольника SO₁E, предварительно вычислив апофему SE

$SE=\sqrt{SD^2-(DC/2)^2}=\sqrt{10^2-5^2}=5\sqrt{3}$

$H=\sqrt{SE^2-r^2}=\sqrt{75-25}=\sqrt{50}=5\sqrt{2}$

Из заданного соотношения найдём радиус шара

$\dfrac{R}{H-R}=\dfrac{r}{\sqrt{H^2+r^2}}~\Rightarrow~\dfrac{R}{5\sqrt{2}-R}=\dfrac{5}{\sqrt{50+25}}$

$R\sqrt{3}=5\sqrt2-R$

$R=\dfrac{5\sqrt{2}}{1+\sqrt3}=\dfrac{5\sqrt{2}(\sqrt3-1)}{2}$

Объём шара: $V=\dfrac{4}{3}\pi R^3=\dfrac{4}{3}\pi\cdot \left(\dfrac{5\sqrt2(\sqrt3-1)}{2}\right)^3=\dfrac{750\sqrt6-1250\sqrt2}{3}\pi$

В правильной четырехугольной пирамиде все ребра равный 10. Найдите объем шара, вписанного в нее

0,0(0 оценок)

Популярные вопросы: Геометрия

Jdudn

10.10.2020 21:59

Впараллелограмме abcd биссектриса острого угла a пересекает сторону bc в точке n, bn=5 см,nc=3см. найдите перриметр параллелограма abcd...

cosovanovcostya

02.09.2020 11:33

С/р по теме признаки подобия треугольникавариант 1no 1.дал от mp i ab, mp4 см, ab-10 см,km - 6 okt.вычислите дазву а.ne 2.дены треугольники мкр и м,к, р. мк.7 см, кр-8...

Princess05082006

04.04.2020 06:24

Найдите площадь треугольника abc сторона ac и bc соответственно равны 12,4 и 8 см, а углы в и с соответственно равны 87градуса и 63градуса....

mbelilovskaa

04.04.2020 06:24

Вравностороннем треугольнике авс на стороне ас отмечены точки д и е . доказать что треугольник две равнобедренный если ад=ес...

герман2031

04.04.2020 06:24

Вкубе abcda1b1c1d1 все ребра равны 4. найдите угол между прямой ad1 и и плоскостью сbd...

Masha110502

27.05.2023 01:23

Утрикутнику abc c=90 ac=9 см,bc=12 см,m- середина ba.пряма dc перпендикулярна площині abc,dc=18 см.знайти dm...

fvgfds

23.03.2021 15:10

Ос бессиктрисы угол сod 54 ° угол вос-? и угол аов-? развернутый угол и...

3класс49

13.04.2023 00:40

Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки, равные 3,6 см и 7,2 см, считая от основания. найдите периметр...

skrlp1234

15.09.2022 16:21

Діагональ перерізу циліндра, який паралельний його осі, дорівнює 12см і утворює з площиною основи кут 60 °. переріз відтинає від кола основи дугу 60 °. знайдіть 1)висоту...

zhanelkenesbekova

15.07.2021 11:06

Средняя линия равностороннего треугольника со стороной 6 см она разбевает его на треугольник и четыреугольник. найдите пириметр четыреугольника...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку