Найдите координаты точек , которые симметричны точке А(4;5)
г) относительно точки S(5;1) ; д) относительно прямой у=3
Объяснение:
г) " Симметрией относительно точки или центральной симметрией относительно точки О называется преобразование плоскости , переводящее точку А в точку А1, что О - середина отрезка АА1 "
Поэтому , точка S -середина АА1 , где А1(х;у)-симметричная точка.
По формулам х=(х₁+х₂):2 ,у=(у₁+у₂):2 , где (х₁;у₁), (х₂;у ₂) -координаты концов отрезка , (х;у ), -координаты середины , получаем
5=(4+х₂):2 , 1=(5+у₂):2 ;
10=4+х₂ , 2=5+у₂ ;
х₂=6 , у₂=-3 ;
А2(6; -3).
д) у(А)=5 , значит расстояние от точки А до прямой у=3 равно 5-3=2 .
Поэтому расстояние от прямой до точки А1 должно быть тоже 2. Абсцисса ,симметричной точки, сохраняется. Значит координаты А1(4;2)
Пусть A (2;3) B (-1;2). найдите координаты точки, которая делит отрезок ab в отношении 1) лямбда=1 ; 2) лямбда = 1/2
Объяснение:
Пусть координаты С(х;у)
1) λ=1 значит, что АС=СВ и С-середина отрезка.
С( (2-1):2 ;(3+2):2 ) , С( 0,5 ; 2,5);
2) λ = 1/2
х=(х₁+λх₂):(1+λ) , у=( у₁+λу₂):(1+λ;
х=(2+1/2*(-1)):(1+1/2) , у=(3+1/2*2):(1+1/2)
х= 1,5: 1,5 , у=4 :1,5
х=1 , у=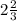
С(1 ;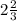 ).
).
======================
х=(х₁+λх₂):(1+λ) ,у=( у₁+λу₂):(1+λ) ,где (х₁;у₁), (х₂;у ₂) -координаты концов отрезка , (х;у)-координаты точки, делящей отрезок в заданном отношении.
Найдите координаты точек , которые симметричны точке А(4;5)
г) относительно точки S(5;1) ; д) относительно прямой у=3
Объяснение:
г) " Симметрией относительно точки или центральной симметрией относительно точки О называется преобразование плоскости , переводящее точку А в точку А1, что О - середина отрезка АА1 "
Поэтому , точка S -середина АА1 , где А1(х;у)-симметричная точка.
По формулам х=(х₁+х₂):2 ,у=(у₁+у₂):2 , где (х₁;у₁), (х₂;у ₂) -координаты концов отрезка , (х;у ), -координаты середины , получаем
5=(4+х₂):2 , 1=(5+у₂):2 ;
10=4+х₂ , 2=5+у₂ ;
х₂=6 , у₂=-3 ;
А2(6; -3).
д) у(А)=5 , значит расстояние от точки А до прямой у=3 равно 5-3=2 .
Поэтому расстояние от прямой до точки А1 должно быть тоже 2. Абсцисса ,симметричной точки, сохраняется. Значит координаты А1(4;2)