Используя символы, запишите соедующее предложение: a иb лежатв плоскости a , аттчка c вне ее(сделать чертеж)

Показать ответ

Ответ:

орлыварив

01.05.2021 08:30

Параллелограммом называется четырёхугольник у которого противоположные стороны попарно равны и параллельны.
Периметр=2(ав+сд)
Сумма углов пар.м.=360°
Сумма односторонних углов,прилежащих к одно стороне=180°
Диагонали пар.м. точкой пересечения делятся пополам.
Трапецией называется четырехугольник у которого 2 стороны параллельны,а другие не параллельны.Параллельные стороны являются основанием,а другие-боковыми сторонами
Трапеция бывает равнобокой/равнобедренной(боковые стороны равны) и прямоугольной(1 угол=90°)
Сумма углов=360°
Сумма односторонних углов при каждом из оснований равна=180°

0,0(0 оценок)

Ответ:

dedmoros1234567

02.01.2023 13:45

Фронталь - это прямая, параллельная фронтальной плоскости : f║XOZ, значит, координата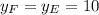 y_F=y_E=10 ⇒ F(15, 10, 40)

Чтобы найти длину стороны квадрата, нужно найти расстояние от точки А до фронтали f.

1) Направляющий вектор фронтали f :

$\vec {EF}=(x_F-x_E; y_F-y_E; z_F-z_E)=(15-70; 10-10; 40-10)\\ \\ \vec {EF}(-55;0;30)\\ \\ |\vec {EF}|=\sqrt{(-55)^2+0^2+30^2} =\sqrt{3925}\approx 62,65$

2) Вектор к точке на фронтали, проходящий через точку A

$\vec {AE} = (70-65;10-20;10-10)=(5;-10;0)$

3) Векторное произведение

$[\vec {AE}\times \vec {EF}]=~\begin{vmatrix} \vec i ~~~~~\vec j ~~~~~\vec k\\ \ ~~5~~-10~~~0 \\ \ -55~~~0~~~30\\ \end{vmatrix}=-300\vec i-550\vec k-150\vec j\\$

$[\vec {AE}\times \vec {EF}]=(-300; -150; -550)$

$|[\vec {AE}\times \vec {EF}]|=\sqrt{(-300)^2+(-150)^2+(-550)^2}=\sqrt{415000}\approx 644,20$

4) Длина стороны квадрата - расстояние от точки А до фронтали

644,20 : 62,65 ≈ 10,28

5) Координаты точки В.

Точка В лежит на фронтали ⇒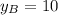 y_B=10

$\dfrac{x-70}{-55}=\dfrac{y-10}{0}=\dfrac{z-10}{30}\\ \\ \dfrac{x_B-70}{-55}=\dfrac{z_B-10}{30}\\ \\ 6(x_B-70)=-11(z_B-10)$

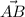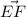С другой стороны векторы $\vec {AB}$ и $\vec {EF}$ перпендикулярны, скалярное произведение равно нулю.

$\vec {AB}=(x_B-65; 10-20; z_B-10)=(x_B-65; -10; x_B-10)$

$\vec {AB} \cdot \vec{EF}=(x_B-65)\cdot (-55)+(-10)\cdot 0 + (z_B-10)\cdot 30=0\\\\\displaystyle \left \{ {{6(x_B-70)=-11(z_B-10)}\atop {-11(x_B-65)+6(z_B-10)=0}}\\\right. ~~\Leftrightarrow~~ \displaystyle \left \{ {{6x_B-420=-11z_B+110}\atop {-11x_B+715+6z_B-60=0}}\\\right. \\\\ \\\displaystyle \left \{ {{6x_B+11z_B+530=0}\atop {-11x_B+6z_B+655=0}}\\\right.$

Решив систему, получаем координаты точки В (66,15; 10; 12,10)

Чтобы не искать координаты точек C и D, достаточно отложить от точки В длину стороны квадрата 10,28 на фронтальной плоскости. Так как ВС║XOZ, то проекция длины квадрата на фронтальную плоскость будет равна длине квадрата. Отложить можно в обе стороны. Возможно 2 варианта построения. В приложении дан чертёж для случая, когда точки C и D расположены к центру координат от точек A и B.