В равнобедренном треугольнике, высота опускается из вершины треугольника на основание и является медианой и биссектрисой. Также известно, что биссектриса делит основание на две равные части.
Чтобы найти радиус вписанной окружности, нужно воспользоваться формулой для нахождения радиуса вписанной окружности в равнобедренный треугольник: R = a * sin(α/2), где a - длина стороны треугольника, α - угол при основании треугольника.
У нас есть сторона треугольника (основание) и боковая сторона равная 20 см. Так как треугольник равнобедренный, то боковая сторона равна одной из сторон треугольника.
Для начала найдем угол при основании треугольника. В равнобедренном треугольнике медиана и биссектриса, опущенные из вершины треугольника на основание, делят угол при вершине на два равных угла. Поэтому можем применить теорему синусов:
sin(α/2) = (a/2) / (боковая сторона), где a - длина стороны треугольника, α - угол при основании треугольника.
sin(α/2) = (32/2) / 20 = 16/20 = 0.8
Теперь мы можем найти радиус вписанной окружности, используя формулу:
R = a * sin(α/2) = 20 * 0.8 = 16 см
Таким образом, радиус вписанной окружности равен 16 см.
Чтобы найти радиус описанной окружности, можно воспользоваться формулой для нахождения радиуса описанной окружности в равнобедренном треугольнике: R = (a/2) / cos(α/2)
Воспользуемся уже найденными значениями стороны треугольника (основание) и угла при основании треугольника, чтобы найти радиус описанной окружности:
R = (32/2) / cos(α/2)
Чтобы найти cos(α/2), воспользуемся формулой для cos(α/2) с использованием тангенса:
tan(α/2) = (a/2) / (боковая сторона), где a - длина стороны треугольника, α - угол при основании треугольника.
tan(α/2) = (32/2) / 20 = 16/20 = 0.8
Зная значение tan(α/2), мы можем найти cos(α/2) из соотношения:
cos(α/2) = 1 / √(1 + tan^2(α/2)), где α - угол при основании треугольника.
1)Найдём BP и AK по теореме Пифагора:
BP=√BO²-OP²=√33²-22²=11√5
AK=√AO²-OK²=√77²-22²=33√5
Отсюда можно найти AB=33√5+11√5=44√5
2)Заметим, что BH=BP(как отрезки касательных,проведённых из одной точки)
Вспомним, что центр вписанной окр.-точка пересечения биссектрис треугольника, поэтому найдём синус угла ABC, используя этот факт:
sin2α=2sinαcosα=2*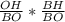 =
=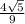
Пусть CP=CK=x,
Тогда SΔ=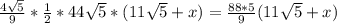
С другой стороны, SΔ=S(ABO)+S(AOC)+S(BOC)
SΔ=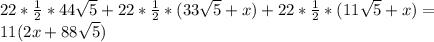
Приравнивая два вышенаписанных выражения для площади, найдём, что x=16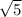 .
.
3)Тогда CO можно найти по теореме Пифагора:
CO=√OK²+CK²= √196*9=42
Чтобы найти радиус вписанной окружности, нужно воспользоваться формулой для нахождения радиуса вписанной окружности в равнобедренный треугольник: R = a * sin(α/2), где a - длина стороны треугольника, α - угол при основании треугольника.
У нас есть сторона треугольника (основание) и боковая сторона равная 20 см. Так как треугольник равнобедренный, то боковая сторона равна одной из сторон треугольника.
Для начала найдем угол при основании треугольника. В равнобедренном треугольнике медиана и биссектриса, опущенные из вершины треугольника на основание, делят угол при вершине на два равных угла. Поэтому можем применить теорему синусов:
sin(α/2) = (a/2) / (боковая сторона), где a - длина стороны треугольника, α - угол при основании треугольника.
sin(α/2) = (32/2) / 20 = 16/20 = 0.8
Теперь мы можем найти радиус вписанной окружности, используя формулу:
R = a * sin(α/2) = 20 * 0.8 = 16 см
Таким образом, радиус вписанной окружности равен 16 см.
Чтобы найти радиус описанной окружности, можно воспользоваться формулой для нахождения радиуса описанной окружности в равнобедренном треугольнике: R = (a/2) / cos(α/2)
Воспользуемся уже найденными значениями стороны треугольника (основание) и угла при основании треугольника, чтобы найти радиус описанной окружности:
R = (32/2) / cos(α/2)
Чтобы найти cos(α/2), воспользуемся формулой для cos(α/2) с использованием тангенса:
tan(α/2) = (a/2) / (боковая сторона), где a - длина стороны треугольника, α - угол при основании треугольника.
tan(α/2) = (32/2) / 20 = 16/20 = 0.8
Зная значение tan(α/2), мы можем найти cos(α/2) из соотношения:
cos(α/2) = 1 / √(1 + tan^2(α/2)), где α - угол при основании треугольника.
cos(α/2) = 1 / √(1 + 0.8^2) ≈ 1 / √(1 + 0.64) ≈ 1 / √1.64 ≈ 0.79
Теперь мы можем найти радиус описанной окружности, используя формулу:
R = (32/2) / cos(α/2) = 16 / 0.79 ≈ 20.25 см
Таким образом, радиус описанной окружности равен примерно 20.25 см.