Из точки A за плосткостью (Альфа) проведены к данной плоскости две равные наклонниые. Отрезок, который соедениняет основания наклонных, равен (a) и образует вместе с наклонной угол (Альфа), а с ее проекцией - угол (Бета). Найти расстояние от точки M до плоскости треугольника.

SM = 4 cм

Объяснение:

найдем гипотенузу основания по теореме Пифагора

АВ=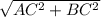 =10

SO высота пирамиды, а OK,OM,ON - серединные перпендикуляры и радиусы вписанной окружности, равные между собой.

Чтобы найти радиус, воспользуемся формулой площади S=pr и

S=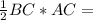0,5*6*8=24 см^2 Тогда r=S/p, где р- полупериметр =(6+8+10)/2=12, r=24:12=2 см

Треугольник SOM прямоугольный с углом 60 и 30 градусов, при вершине угол 30 градусов, катет напротив этого угла равен половине гипотенузы, значит гипотенуза (высота боковой грани)  SM = 2r=4 cм

Если аб основание, тогда св боковая сторона, поскольку трапеция р/б, то св = ад = 10см, Проведём высоты из вершины тупых углов к большему основанию, обазначим их, как СМ и ДН. Получили два прямоугольных треугольника, которые равны по трём углам. Поскольку в р/б трапеции углы при основании равны, значит угол БСМ = углу АДН = 30градусам. АН и БМ из равенства треугольников равны. Также они лежат напротив угла в 30 градусов, соответсвенно равны 1/2 гипотенузы Т.е СВ, значит они равны 5 см. У нас остаётся отрезок МН = СД по свойству р/б трапеции. Поскоьку АБ=16, а АН и БМ 5 см, то НМ = СД = 6 см ответ: СД = 6 см