Из точки М, лежащей внутри угла АВС, проведены перпендикуляры МК и МР к сторонам угла. Угол АВС=60 градусов. МК=4см, ВМ=8см. определите вид треугольника АВС;
Площадь поверхности усечённого конуса вычисляется по формуле:
S = п * (r1 + r2) * l + п * r12 + п * r22.
Здесь r1 и r2 — радиусы оснований, l — образующая.
Для начала, вычислим радиусы оснований:
4 * п = 2 * п * r1;
r1 = 2;
10 * п = 2 * п * r2;
r2 = 5.
Теперь опустим высоту из крайней точки меньшего основания на большее. Мы получим прямоугольный треугольник, один из катетов которого равен высоте, а другой — разности радиусов. Найдём его:
5 - 2 = 3.
По теореме Пифагора можно найти образующую:
l = sqrt (9 + 16) = 5.
Тогда площадь полной поверхности усечённого конуса будет равна:
S = п * (2 + 5) * 5 + п * 4 + п * 25 = 64 * п.
ответ: площадь полной поверхности усечённого конуса равна 64 * п
Так как AD - общая для данных треугольников, то медианы пересекут AD в точке О.
Медиана, проведенная из прямого угла прямоугольного треугольника к гипотенузе, равна половине гипотенузы.
⇒ АО = OD = OC = OB.
⇒ точки A, B, C, D будут лежать на одной окружности, то есть вокруг данной трапеции можно описать окружность.
Если вокруг трапеции можно описать окружность, то трапеция равнобедренная.
⇒ АВ = CD
Проведем высоту ВН.
В равнобедренной трапеции высота, опущенная из вершины тупого угла на основание, делит это основание на отрезки, меньшее из которых равно полуразности оснований.
Площадь поверхности усечённого конуса вычисляется по формуле:
S = п * (r1 + r2) * l + п * r12 + п * r22.
Здесь r1 и r2 — радиусы оснований, l — образующая.
Для начала, вычислим радиусы оснований:
4 * п = 2 * п * r1;
r1 = 2;
10 * п = 2 * п * r2;
r2 = 5.
Теперь опустим высоту из крайней точки меньшего основания на большее. Мы получим прямоугольный треугольник, один из катетов которого равен высоте, а другой — разности радиусов. Найдём его:
5 - 2 = 3.
По теореме Пифагора можно найти образующую:
l = sqrt (9 + 16) = 5.
Тогда площадь полной поверхности усечённого конуса будет равна:
S = п * (2 + 5) * 5 + п * 4 + п * 25 = 64 * п.
ответ: площадь полной поверхности усечённого конуса равна 64 * п
8 ед.
Объяснение:
Дано: ABCD - трапеция.
∠ABD = ∠ACD = 90°
AB = 2, BC = 7.
Доказать: АВ = CD;
Найти: АD.
Доказательство:
Рассмотрим ΔABD и ΔACD - прямоугольные.
Проведем медианы ВО и СО соответственно.
Так как AD - общая для данных треугольников, то медианы пересекут AD в точке О.
Медиана, проведенная из прямого угла прямоугольного треугольника к гипотенузе, равна половине гипотенузы.
⇒ АО = OD = OC = OB.
⇒ точки A, B, C, D будут лежать на одной окружности, то есть вокруг данной трапеции можно описать окружность.
Если вокруг трапеции можно описать окружность, то трапеция равнобедренная.
⇒ АВ = CD
Проведем высоту ВН.
В равнобедренной трапеции высота, опущенная из вершины тупого угла на основание, делит это основание на отрезки, меньшее из которых равно полуразности оснований.
⇒ АН = (АD-ВС):2 = (AD-7):2
Пусть АН = х, тогда х = (AD-7):2
или AD=2x+7
Рассмотрим ΔАВН и ΔABD - прямоугольные.
∠А - общий.
⇒ ΔАВН ~ ΔABD (по двум углам)
Составим пропорцию:
x₂ - не подходит
⇒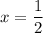
AD = 2x+7 = 8(ед)