Обозначим данные точки А, В и С. Эти три точки можно соединить одним единственным в фигуру из трех точек и трех отрезков. Т.е. в треугольник , для которого предлагается построить два подобных с коэффициентом подобия k=3 и k=0,5 ( См. рисунки вложения)
Продлим ВС и АС и с циркуля 3 раза отложим длину этих сторон. Получим СА1=3АС и СВ1=3ВС. Угол А1СВ1 получившегося треугольника равен углу ВСА ( вертикальные). Треугольники АВС и А1В1С подобны по пропорциональным сторонам и равному углу между ними. Аналогично строится треугольник А2СВ2, подобный треугольника АВС с k=0,5. Для этого сначала делим две стороны пополам деления отрезка пополам циркулем Вы, конечно, уже знаете).
На сторонах угла ВАС от А циркулем на АС и АВ откладываем равные отрезки АМ и АК. Соединим М и К. На произвольной прямой отмечаем т.А1 и чертим окружность радиусом, равным АК. Точку пересечения с взятой прямой отмечаем К1. От К1 на окружности циркулем отмечаем точку М1 так, что К1М1=КМ. Из центра А1 окружности поводим прямую А1М1. Угол, равный углу ВАС исходного треугольника, построен. На прямых А1М1 и А1К1 откладываем стороны нужной длины: А1С1=3АС и А1В1=3 ВС и соединяем их. Аналогично для треугольника с k=0,5 откладываем половины длин сторон АС и АВ треугольника АВС и соединяем их. Стороны построенных треугольников пропорциональны сторонам исходного, а углы между ними равны углу ∆ АВС.
1) Проведём две высоты к плоскости ABCD из вершин и И отметим их как и соответственно.
2)Рассмотрим полученный треугольник ; По чертежу видно, что этот треугольник прямоугольный и один из его острых углов равен 60 градусов, что означает что второй его угол равен 30 градусам, следовательно если нам известна , то можно и найти
(Против угла в 30 градусов лежит катет равный половине гипотенузы).
3)Поскольку пирамида правильная, то высоты, которые были проведены в 1 пункте делят диагональ квадрата ABCD на 3 отрезка, причем
4) Используя правило прямоугольного треугольника, при двух его известных сторонах и углу, можно найти другую сторону этого треугольника:
5)Следует детально рассмотреть треугольник В нем известны две стороны, и он прямоугольный, а значит можно найти по теореме Пифагора. .
6)Отсюда можно найти .
. Знаю эту величину можем найти искомую АB.
Поскольку в основании правильной усеченной четырёхугольной пирамиды лежит квадрат. ; Но также стоит заметить, что , но второй намного легче, чем мучиться с преобразованием корневых выражений.
Обозначим данные точки А, В и С. Эти три точки можно соединить одним единственным в фигуру из трех точек и трех отрезков. Т.е. в треугольник , для которого предлагается построить два подобных с коэффициентом подобия k=3 и k=0,5 ( См. рисунки вложения)
Продлим ВС и АС и с циркуля 3 раза отложим длину этих сторон. Получим СА1=3АС и СВ1=3ВС. Угол А1СВ1 получившегося треугольника равен углу ВСА ( вертикальные). Треугольники АВС и А1В1С подобны по пропорциональным сторонам и равному углу между ними. Аналогично строится треугольник А2СВ2, подобный треугольника АВС с k=0,5. Для этого сначала делим две стороны пополам деления отрезка пополам циркулем Вы, конечно, уже знаете).
На сторонах угла ВАС от А циркулем на АС и АВ откладываем равные отрезки АМ и АК. Соединим М и К. На произвольной прямой отмечаем т.А1 и чертим окружность радиусом, равным АК. Точку пересечения с взятой прямой отмечаем К1. От К1 на окружности циркулем отмечаем точку М1 так, что К1М1=КМ. Из центра А1 окружности поводим прямую А1М1. Угол, равный углу ВАС исходного треугольника, построен. На прямых А1М1 и А1К1 откладываем стороны нужной длины: А1С1=3АС и А1В1=3 ВС и соединяем их. Аналогично для треугольника с k=0,5 откладываем половины длин сторон АС и АВ треугольника АВС и соединяем их. Стороны построенных треугольников пропорциональны сторонам исходного, а углы между ними равны углу ∆ АВС.
Дано:
Найти: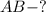
1) Проведём две высоты к плоскости ABCD из вершин
и 
И 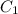отметим их как 
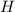и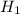 
соответственно.
2)Рассмотрим полученный треугольник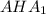
; По чертежу видно, что этот треугольник прямоугольный и один из его острых углов равен 60 градусов, что означает что второй его угол равен 30 градусам, следовательно если нам известна 
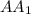, то можно и найти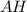 
3)Поскольку пирамида правильная, то высоты, которые были проведены в 1 пункте делят диагональ квадрата ABCD на 3 отрезка, причем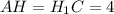
4) Используя правило прямоугольного треугольника, при двух его известных сторонах и углу, можно найти другую сторону этого треугольника: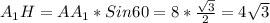
5)Следует детально рассмотреть треугольник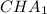
В нем известны две стороны, и он прямоугольный, а значит можно найти 
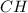по теореме Пифагора. 
.
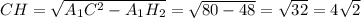6)Отсюда можно найти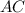
.
Поскольку в основании правильной усеченной четырёхугольной пирамиды лежит квадрат.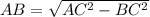
; Но также стоит заметить, что 
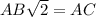, но второй намного легче, чем мучиться с преобразованием корневых выражений.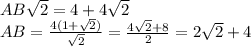 
ответ: AB= двум корней из двух плюс 4