Изобразите тупоугольный треугольник abc, где угол a - тупой. постройте при циркуля и линейки точку пересечения высоты bh и медианы am названного треугольника.
1.Градусная мера дуги, на которую опирается центральный угол, равна 80 °. Определить градусную меру этого угл
а) 120° б) 80° в) 40°г) 50°
Центральный угол равен градусной мере дуги, на которую опирается. Поэтому ответ б) 80 градусов
2.Градусная мера центрального угла равна 120 °. Определить градусную меру дуги, на которую он опирается.
Из аналогичных соображений ответ г) 120 градусов.
а) 160° б) 90° в) 60°г) 120°
3.Градусная мера вписанного угла равна 140 °. Определить градусную меру дуги, на которую он опирается.
Вписанный угол равен половине градусной меры дуги на которую опирается. Поэтому градусная мера дуги равна 140*2 = 280 градусов. ответ в) 280 градусов.
а) 100° б) 70° в) 280°г) 140°
4.Градусная мера дуги, на которую опирается вписанный угол, равна 90°.Определить градусную меру этого вписанного угла.
Из аналогичных соображений, вписанный угол равен половине градусной меры дуги, на которую опирается. Следовательно, угол равен 90/2 = 45 градусов. ответ б) 45 градусов.
а) 100° б) 45° в) 180°г) 90°
5.Определить градусную меру угла, вписанного в окружность, если соответствующий ему центральный угол равен 126 ° .
Центральный угол равен градусной мере дуги, на которую опирается, а вписанный угол половине дуги. Следовательно, вписанный угол равен половине центрального угла, опирающегося на ту же дугу. ответ а) 63 градуса.
а) 63° б) 252° в) 180°г) 126°
6.Определить градусную меру центрального угла окружности, если градусная мера соответствующего ему вписанного угла равна 40 ° .
Из аналогичных рассуждений, центральный угол в 2 раза больше вписанного угла, опирающегося на ту же дугу. ответ г) 80 градусов.
Так как 1 острый угол в нем 60 градусов, то 2 угол в треугольнике равен 90-60=30 градусов ( сумма острых углов 90) . А по правилу, сторона, против угла в 30 градусов, равна половине гипотенузы. Гипотенуза тут - это диагональ. (НО только в нашем случае) Диагональ = 10 Так что половина гипотенузы, то есть меньшая сторона треугольника (и прямоугольника в том числе) равна 0,5*10 =5 ( это одно и тоже, что и 10 : 2 )
А далее нам идет в теорема Пифагора. Круто) =+, где c- гипотенуза, а и b - катеты. нам неизвестно b.
Объяснение:
1.Градусная мера дуги, на которую опирается центральный угол, равна 80 °. Определить градусную меру этого угл
а) 120° б) 80° в) 40°г) 50°
Центральный угол равен градусной мере дуги, на которую опирается. Поэтому ответ б) 80 градусов
2.Градусная мера центрального угла равна 120 °. Определить градусную меру дуги, на которую он опирается.
Из аналогичных соображений ответ г) 120 градусов.
а) 160° б) 90° в) 60°г) 120°
3.Градусная мера вписанного угла равна 140 °. Определить градусную меру дуги, на которую он опирается.
Вписанный угол равен половине градусной меры дуги на которую опирается. Поэтому градусная мера дуги равна 140*2 = 280 градусов. ответ в) 280 градусов.
а) 100° б) 70° в) 280°г) 140°
4.Градусная мера дуги, на которую опирается вписанный угол, равна 90°.Определить градусную меру этого вписанного угла.
Из аналогичных соображений, вписанный угол равен половине градусной меры дуги, на которую опирается. Следовательно, угол равен 90/2 = 45 градусов. ответ б) 45 градусов.
а) 100° б) 45° в) 180°г) 90°
5.Определить градусную меру угла, вписанного в окружность, если соответствующий ему центральный угол равен 126 ° .
Центральный угол равен градусной мере дуги, на которую опирается, а вписанный угол половине дуги. Следовательно, вписанный угол равен половине центрального угла, опирающегося на ту же дугу. ответ а) 63 градуса.
а) 63° б) 252° в) 180°г) 126°
6.Определить градусную меру центрального угла окружности, если градусная мера соответствующего ему вписанного угла равна 40 ° .
Из аналогичных рассуждений, центральный угол в 2 раза больше вписанного угла, опирающегося на ту же дугу. ответ г) 80 градусов.
а) 40° б) 20° в) 140°г) 80°
Так как 1 острый угол в нем 60 градусов, то 2 угол в треугольнике равен 90-60=30 градусов ( сумма острых углов 90) . А по правилу, сторона, против угла в 30 градусов, равна половине гипотенузы. Гипотенуза тут - это диагональ. (НО только в нашем случае) Диагональ = 10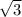
Так что половина гипотенузы, то есть меньшая сторона треугольника (и прямоугольника в том числе) равна 0,5*10
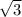=5
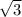( это одно и тоже, что и 10
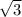: 2 )
А далее нам идет в теорема Пифагора. Круто)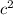
=
+
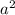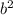, где c- гипотенуза, а и b - катеты. нам неизвестно b.
подставляем
b= 15
А теперь можно найти площадь. S=A*B=15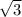*5
=75
ОТВЕТ: 15м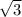, 5
м, 75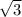
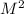
Надеюсь Объяснила суть решения.