Щоб побудувати точку C', у яку перейде точка C внаслідок повороту навколо точки O на кут α=90 градусів, потрібно (дивись рисунок):
а) провести промінь OC;
б) від променя OC відкласти кут COK, що дорівнює куту α у заданому напрямку (за умовою цього завдання – проти годинникової стрілки на кут α=90);
в) на промені OK знайти точку C', яка лежить на відстані OC від центру повороту O. Знайдемо довжини відрізка OC (і відповідно OC'):
Якщо на промені OK від точки O відкласти відрізок |OC'|= √10, то отримаємо координати точки C'(-3;1).
Звичайно, що точно відкласти довжини більшості відрізків не зручно (або неможливо), тому для пошуку координат точки (x';y'), при попороті точки (x;y) на кут α проти годинникової стрілки, зручно використовувати формули:
Щоб побудувати точку C', у яку перейде точка C внаслідок повороту навколо точки O на кут α=90 градусів, потрібно (дивись рисунок):
а) провести промінь OC;
б) від променя OC відкласти кут COK, що дорівнює куту α у заданому напрямку (за умовою цього завдання – проти годинникової стрілки на кут α=90);
в) на промені OK знайти точку C', яка лежить на відстані OC від центру повороту O. Знайдемо довжини відрізка OC (і відповідно OC'):
Якщо на промені OK від точки O відкласти відрізок |OC'|= √10, то отримаємо координати точки C'(-3;1).
Звичайно, що точно відкласти довжини більшості відрізків не зручно (або неможливо), тому для пошуку координат точки (x';y'), при попороті точки (x;y) на кут α проти годинникової стрілки, зручно використовувати формули:
у нашому випадку, отримаємо
Відповідь: (-3;1) – А.
Объяснение:
a = 5 см,
b = 4 см,
c = 7 см.
Найти R.
Запишем теорему синусов:
числитель и знаменатель дроби слева последнего равенства домножим на (b·c).
С учётом того, что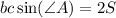
, где S - площадь данного в условии треугольника, имеем
Площадь треугольника можно найти по формуле Герона:
Найдем, сначала, площадь треугольника.
p = (5+4+7)/2 = (9+7)/2 = 16/2 = 8 см.
S = √(8·(8-5)·(8-4)·(8-7)) = √(8·3·4·1) = 4·(√6) см²
Теперь найдем радиус описанной окружности.
R = 5·4·7/(4·4·(√6)) = 5·7/(4·(√6)) = 35·(√6)/(4·6) = 35·(√6)/24 см.
Теперь найдём длину окружности, описанной около данного треугольника.
L = 2πR = 2π·35·(√6)/24 см = π·35·(√6)/12 см.