Известны координаты четырех вершин параллелепипеда abcda1b1c1d1: а) A(1;0;-1),B(2;-1;1),C(3;0;0), C1(1;2;2)
б) A(-2;1;0),C(0;1;2),B1(-3;1;0),D1(-3;0;2)Найдите координаты четырех оставшихся вершин. Для каждого из пунктов а и б найдите: векторAB+вектор CD, вектор AA1+вектор BB1; вектор AB1+векторBC1+векторCD1+вектор DA1.

ответ:  вторая высота равна либо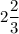     дм , либо  6 дм .

ΔАВС ,  АС=18 дм , АВ=12 дм ,  СМ ⊥ АВ ,  ВР ⊥ АС .

Одна из высот равна 4 дм .

Так как в условии не сказано, какая высота равна 4 дм , то рассмотрим два случая .

1) Пусть задана высота  СМ=4 дм .

Запишем, чему равна площадь ΔАВС в двух вариантах.

S=0,5*AB*CM = 0,5*AC*BP    ⇒     АВ*СМ=АС*ВР  .

Заменим стороны и высоту известными числами .

12*4=18*ВР  ,  48=18*ВР  ,  ВР=48:18=2 и 2/3 дм

2)  Пусть задана высота ВР=4 дм .

Аналогично имеем  АВ*СМ=АС*ВР  ,   12*СМ=18*4  ,  12*СМ=72  ,

 СМ=72:12=6 дм

≈3.91 (не уверен)

Объяснение:

так как треугольник АВЕ равнобедренный то стороны АВ и ЕВ равны

АВ=ЕВ = 1.5

по теореме пифагора найдем сторону АЕ =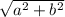 = = 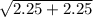 ≈ 2,1

теперь  надо найти сторону ED

у нас есть две стороны 2.1 и 5.1, а узнать угол между ними мы узнаем из того что сторона AE треугольника ABE делит угол А на 2 угла, а значит каждый угол имеет 45 градусов

не уверен насчет насколько правильно найдена сторона ED, но я уже просто не знаю как по другому найти, замена 2.1 на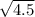 тоже сильно не , так что вот