Көмек керек отиниш акконил еринбей көмектесиниздерши ага-апкелерим көмек кутемин отиниш сиздерге жаксылыктарыныз алладан кайтсин қатты керек сабақта болмай тақырып тусинбей қалдым алдын ала рахмет
Нехай задано рівнобічну трапецію ABCD, основи паралельні AD||BC, сторони AB=CD рівні між собою, BH⊥AD, де BH=12 см – висота трапеції, опущена на сторону AD,
AH=5 см, HD=11 см, звідси AD=AH+HD=5+11=16 см.
Розглянемо прямокутний трикутник ABH (∠AHB=90) та знайдемо за формулою Піфагора гіпотенузу AB:
AB^2=AH^2+BH^2, звідси
Оскільки трапеція ABCD – рівнобічна, то відповіні сторони рівні CD=AB=13 см.
Опустимо ще одну висоту CK на сторону AD, тоді кут прямий CK⊥AD (∠CKD=90).
Розглянемо прямокутні трикутники ABH і KCD.
У них ∠BAH=∠CKD – як кути при основі AD у рівнобічній трапеції ABCD (за властивістю), і CD=AB=13 см.
Тому, за ознакою рівності прямокутних трикутників, трикутники ABH і KCD рівні (за гіпотенузою і гострим кутом), звідси слідує AH=KD=5 см.
Дано: ABCD - параллелограмм. , AK=64 см, KD=225 cм, .
Найти: BD
Решение: Треугольник АВD является прямоугольным, так как BD перпендикулярно DC. A DC||AB. Значит BD является секущей при параллельных АВ и CD. Поэтому
Есть такое свойство в прямоугольном треугольнике, что высота, проведенная к гипотенузе, является средним геометрическим отрезков, на которое делит высота гипотенузу.
BK=120 см.
Теперь по теореме Пифагора BD - гипотенуза треугольника BKD.
Нехай задано рівнобічну трапецію ABCD, основи паралельні AD||BC, сторони AB=CD рівні між собою, BH⊥AD, де BH=12 см – висота трапеції, опущена на сторону AD,
AH=5 см, HD=11 см, звідси AD=AH+HD=5+11=16 см.
Розглянемо прямокутний трикутник ABH (∠AHB=90) та знайдемо за формулою Піфагора гіпотенузу AB:
AB^2=AH^2+BH^2, звідси
Оскільки трапеція ABCD – рівнобічна, то відповіні сторони рівні CD=AB=13 см.
Опустимо ще одну висоту CK на сторону AD, тоді кут прямий CK⊥AD (∠CKD=90).
Розглянемо прямокутні трикутники ABH і KCD.
У них ∠BAH=∠CKD – як кути при основі AD у рівнобічній трапеції ABCD (за властивістю), і CD=AB=13 см.
Тому, за ознакою рівності прямокутних трикутників, трикутники ABH і KCD рівні (за гіпотенузою і гострим кутом), звідси слідує AH=KD=5 см.
Тоді у рівнобічній трапеції:
HK=HD-KD=11-5=6 см, тому BC=HK=6 см.
Знайдемо периметр рівнобічної трапеції ABCD:
P=AB+BC+CD+AD=13+6+13+6=48 см.
Відповідь: 48 см – В.
Дано: ABCD - параллелограмм. , AK=64 см, KD=225 cм,
, AK=64 см, KD=225 cм, 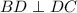 .
.
Найти: BD
Решение: Треугольник АВD является прямоугольным, так как BD перпендикулярно DC. A DC||AB. Значит BD является секущей при параллельных АВ и CD. Поэтому
Есть такое свойство в прямоугольном треугольнике, что высота, проведенная к гипотенузе, является средним геометрическим отрезков, на которое делит высота гипотенузу.
BK=120 см.
Теперь по теореме Пифагора BD - гипотенуза треугольника BKD.
ответ: BD=255 cм.