Геометрия: Көмектесіңдерші тез арада өтінемін

Көмектесіңдерші тез арада өтінемін

Показать ответ

Ответ:

EfaliyaRom

01.05.2020 02:38

Найдите тангенс угла В в треугольнике АВС, изображённого на рисунке.

- - -

Возьмём длину клеточки за 1 (ед).

Достраиваем ΔАВС до прямоугольника АОНМ как показано на рисунке.

1) Рассмотрим прямоугольный ΔАОВ.

АВ - гипотенуза, так как лежит против угла в 90°.

АО = 5 (ед) (так как занимает 5 клеточек).

ОВ = 1 (ед) (так как занимает 1 клеточку).

По теореме Пифагора находим гипотенузу АВ -

$AB=\sqrt{AO^{2}+OB^{2} } \\\\AB=\sqrt{5^{2}+1^{2} } \\\\AB=\sqrt{25+1 } \\\\AB=\sqrt{26}$

AB = √26 (ед).

Далее по аналогии рассматриваем другие прямоугольные треугольники (а именно ΔВНС и ΔАМС).

2) Рассмотрим прямоугольный ΔВНС.

ВС - гипотенуза.

ВН = 2 (ед).

НС = 2 (ед).

Тогда -

$BC=\sqrt{BH^{2}+HC^{2} }\\\\BC=\sqrt{2^{2}+2^{2} }\\\\BC=\sqrt{4+4 }\\\\BC=\sqrt{8 }$

BC = √8 (ед).

3) Рассмотрим прямоугольный ΔАМС.

АС - гипотенуза.

СМ = 3 (ед).

АМ = 3 (ед).

Тогда -

$AC=\sqrt{CM^{2}+AM^{2} } \\\\AC=\sqrt{3^{2}+3^{2} }\\\\AC=\sqrt{9+9 }\\\\AC=\sqrt{18 }$

AC = √18 (ед).

Теперь рассмотрим весь ΔАВС.

Если сумма квадратов меньших сторон равна квадрату большей стороны, то такой треугольник - прямоугольный.

Теперь проверяем на верность следующие равенство -

$AB^{2} =AC^{2} +BC^{2} \\\\(\sqrt{26})^{2} =(\sqrt{18})^{2} +(\sqrt{8})^{2} \\\\26 = 18+8\\\\26=26$

Равенство верно. Следовательно, ΔАВС - прямоугольный.

Так как АВ - большая сторона (гипотенуза), то ∠АСВ = 90°.

Тангес острого угла прямоугольного треугольника - отношение противолежащего катета к прилежащему.

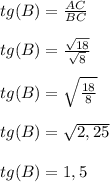
$tg(B)=\frac{AC}{BC} \\\\tg(B)=\frac{\sqrt{18} }{\sqrt{8} } \\\\tg(B)=\sqrt{\frac{18}{8} } \\\\tg(B)=\sqrt{2,25 }\\\\tg(B)=1,5$

ответ :

1,5.

Номер 19.Найдите тангенс угла B в треугольнике ABC, изображённого на рисунке

0,0(0 оценок)

Ответ:

NikolayMakaren

18.03.2021 09:54

Будем считать, что задание звучит так:

В основе четырехугольной пирамиды лежит ромб с диагоналями 6 см и 8 см, а боковые грани наклонены к основанию под углом 45 °. Вычислить объем пирамиды.

Сторона a основания вычисляется по Пифагору:

а = √((6/2)² + (8/2)²) = 5.

Проекция высоты боковой грани на основание равна высоте h треугольника как (1/4) части ромба.

h = 2S/a = 2*(1/2)*3*4/5 = 12/5 = 2,4.

Так как боковые грани наклонены к основанию под углом 45°, то высота пирамиды Н равна h/

Площадь основания So = (1/2)d1*d2 = (1/2)*6*8 = 24 см².

Получаем ответ:

Объем пирамиды V = (1/3)SoH = (1/3)*24*2,4 = 19,2 см³.

0,0(0 оценок)

Популярные вопросы: Геометрия