2. Площадь параллелограмма S = a*h, где a - основание, а h - высота. Поскольку дана большая высота, то основанием является меньшая сторона (поскольку шлощадь неизменна, то для большей стороны высота будет меньшей).
S = 12*7 = 84 см²
3. Площадь равнобедренного треугольника S = (1/2)*b*h, где b - основание, а h - высота. Известна боковая сторона - а и высота h. Боковая сторона, высота и половина основания образуют прямоугольный треугольник. Применяем теорему Пифагора:
35°, 52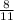
°, 92
°
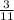Объяснение:
1) <BOC = 70°, => <BAC = 70° : 2 = 35° по свойству вписанного угла.
Т.к. <BOC = 70°, то дуга BC = 70° тоже по свойству центрального угла, тогда на дуга BAC = 360° - 70° = 290°.
2) По условию AB : AC = 4:7, => дуга AB + дуга AC = 4x + 7x = 290°
11x = 290°
x = 290 : 11 = 26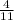
°
3) Дуга AB = 4x = 4*26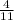
= 105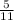 
, => <BCA, опирающийся на дугу AB в 2 раза меньше дуги AB по свойству вписанного угла, => <BCA = 105 
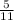: 2 = 52
°
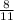4) Дуга AC = 7x = 7*26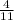
= 184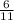 
, => <ABC, опирающийся на дугу AC в 2 раза меньше дуги AC по свойству вписанного угла, => <ABC = 184 
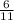: 2 = 92
°
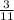1. в) 1440°
2. а) 84 см²
3. г) 108 см²
Объяснение:
1. Суммы углов выпуклого n-угольника = 180°(n-2)
Для n = 10, Сумма углов = 180°*8 = 1440°
2. Площадь параллелограмма S = a*h, где a - основание, а h - высота. Поскольку дана большая высота, то основанием является меньшая сторона (поскольку шлощадь неизменна, то для большей стороны высота будет меньшей).
S = 12*7 = 84 см²
3. Площадь равнобедренного треугольника S = (1/2)*b*h, где b - основание, а h - высота. Известна боковая сторона - а и высота h. Боковая сторона, высота и половина основания образуют прямоугольный треугольник. Применяем теорему Пифагора:
a² = (b/2)² + h² => b = 2*√(a² - h²) = 2*√15² - 9² = 2*12 = 24
S = (1/2)*24*h = 108 см²